
分析 (Ⅰ)由$|{\vec a}|$=1,$|{\vec b}|$=1,$\vec a$与$\vec b$的夹角为60°,再根据向量模的性质即可求出向量$\vec c$和$\vec d$的模;
(Ⅱ)设向量$\vec c$和向量$\vec d$的夹角为θ,再求出$\overline{c}•\overline{d}$的值,则cosθ=$\frac{\overrightarrow{c}•\overrightarrow{d}}{|\overrightarrow{c}||\overrightarrow{d}|}$,代值计算即可求出向量$\vec c$和向量$\vec d$的夹角.
解答 解:(Ⅰ)∵$|{\vec a}|$=1,$|{\vec b}|$=1,$\vec a$与$\vec b$的夹角为60°,
∴$|\overrightarrow{c}|=\sqrt{{\overrightarrow{c}}^{2}}$=$\sqrt{(2\overrightarrow{a}-b)^{2}}=\sqrt{4{\overrightarrow{a}}^{2}-4|\overrightarrow{a}||\overrightarrow{b}|cos60°+{\overrightarrow{b}}^{2}}$=$\sqrt{4-4×1×1×\frac{1}{2}+1}=\sqrt{3}$;
$|\overrightarrow{d}|=\sqrt{{\overrightarrow{d}}^{2}}$=$\sqrt{(\overrightarrow{a}-2\overrightarrow{b})^{2}}$=$\sqrt{{\overline{a}}^{2}-4|\overline{a}||\overline{b}|cos60°+4{\overline{b}}^{2}}$=$\sqrt{1-4×1×1×\frac{1}{2}+4×1}=\sqrt{3}$;
(Ⅱ)设向量$\vec c$和向量$\vec d$的夹角为θ,
∵$\overline{c}•\overline{d}$=$(2\overline{a}-\overline{b})•(\overline{a}-2\overline{b})$=$2{\overline{a}}^{2}-5|\overline{a}||\overline{b}|cos60°+2{\overline{b}}^{2}$=$2-5×\frac{1}{2}+2=\frac{3}{2}$,
∴cosθ=$\frac{\overrightarrow{c}•\overrightarrow{d}}{|\overrightarrow{c}||\overrightarrow{d}|}$=$\frac{\frac{3}{2}}{\sqrt{3}×\sqrt{3}}=\frac{1}{2}$,即θ=$\frac{π}{3}$.
∴$\vec c$和向量$\vec d$的夹角为$\frac{π}{3}$.
点评 本题主要考查平面向量数量积的运算,考查了向量的模的求法以及求两个向量的夹角,两个向量数量积的定义,属于中档题.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)6 | B. | C${\;}_{6}^{3}$($\frac{1}{2}$)6 | C. | C${\;}_{6}^{3}$($\frac{1}{2}$)3 | D. | C${\;}_{6}^{3}$C${\;}_{6}^{3}$($\frac{1}{2}$)6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
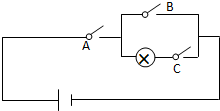 如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )
如图所示电路,有A、B、C三个开关,每个开关开或关的概率都是$\frac{1}{2}$,且相互独立,则灯泡亮的概率( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(0)=2 | B. | 函数f(x)是偶函数 | C. | 函数f(x)是奇函数 | D. | [f(x)+1][f(x)-1]=f(2x)+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥 P-ABCD中,底面 ABCD为矩形,PA⊥平面ABCD,点 E在线段 PC上,PC⊥平面 BDE.
如图,在四棱锥 P-ABCD中,底面 ABCD为矩形,PA⊥平面ABCD,点 E在线段 PC上,PC⊥平面 BDE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com