考点:数学归纳法,归纳推理
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(Ⅰ)通过已知条件,直接求解f(1)、f(2)、f(3);
(Ⅱ)先假设存在符合题意的常数a,b,c,再令n=1,n=2,n=3构造三个方程求出a,b,c,再用用数学归纳法证明成立,证明时先证:①当n=1时成立.②再假设n=k(k≥1)时,成立,即
| 12•1+22•3+…n2•(2n-1) |
| n(n+1) |
=an
2+bn+c,再递推到n=k+1时,成立即可.
解答:
解:(Ⅰ)函数f(n)=
| 12•1+22•3+…n2•(2n-1) |
| n(n+1) |
,f(1)=
;f(2)=
;f(3)=
;
(Ⅱ)假设存在符合题意的常数a,b,c,由(Ⅰ)可得:
,解得:a=
,b=
,c=
-;
证明:①的n=1,2,3时已经证明等式成立;
②假设n=k(k≥3)时,等式成立,即f(k)=
(3k2+k-1).
则当n=k+1时,
f(k+1)=
| 12•1+22•3+…+k2•(2k-1)+(k+1)2(2k+1) |
| (k+1)(k+2) |
=
| 12•1+22•3+…+k2•(2k-1) |
| (k+1)(k+2) |
+=
•+=
=
(k+2)(3k2+7k+3)=
[3(k+1)2+(k+1)-1]∴当n=k+1时,等式也成立.
综上所述,当a=
,b=
,c=
-时,题设的等式对于一切正整数n都成立.
点评:第(Ⅰ)题主要考查递推公式的应用,第(Ⅱ)题主要考查研究存在性问题和数学归纳法,对存在性问题先假设存在,再证明是否符合条件.数学归纳法的关键是递推环节,要符合假设的模型才能成立.



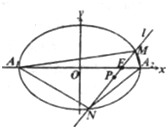 已知椭圆C:
已知椭圆C: