
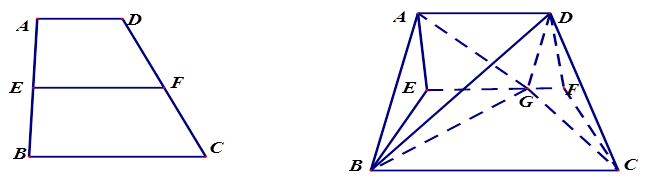
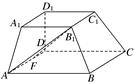
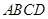 中,
中, ,点
,点 分别是
分别是 的中点,点
的中点,点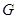 在
在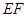 上,沿
上,沿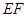 将梯形
将梯形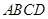 翻折,使平面
翻折,使平面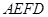
 平面
平面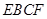 .
.
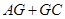 最小时,求证:
最小时,求证: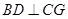 ;
; 时,求二面角
时,求二面角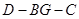 平面角的余弦值.
平面角的余弦值.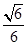
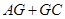 最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相关向量,即可判断直线的垂直关系.
最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相关向量,即可判断直线的垂直关系.
 、
、 分别是
分别是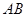 、
、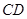 的中点,∴EF//BC
的中点,∴EF//BC 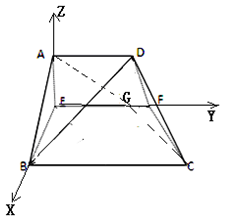
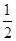 BC=2,又∵EA=EB=2.
BC=2,又∵EA=EB=2. 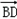 =(﹣2,2,2),
=(﹣2,2,2),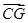 =(-2,-2,0)
=(-2,-2,0)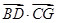 =(﹣2,2,2)(-2,-2,0)=0,
=(﹣2,2,2)(-2,-2,0)=0,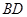 ⊥
⊥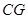
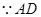 ∥平面
∥平面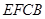 ,
, 点D到平面EFCB的距离为即为点A到平面EFCB的距离.
点D到平面EFCB的距离为即为点A到平面EFCB的距离.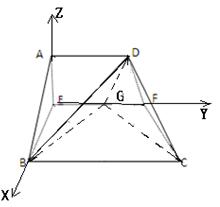
 [(3- k)+4]×2=7-k
[(3- k)+4]×2=7-k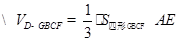 =
=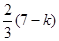
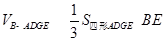 =
=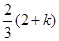 ,
,
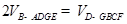 ,
,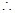
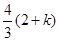 =
=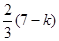 ,
,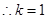 即EG=1
即EG=1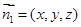 ,∵G(0,1,0),
,∵G(0,1,0),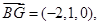
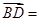 (-2,2,2),
(-2,2,2), 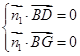 ,即
,即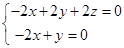
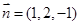
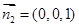
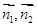 >=
>=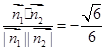 由于所求二面角D-BF-C的平面角为锐角,
由于所求二面角D-BF-C的平面角为锐角,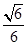
 EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD.
EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD. 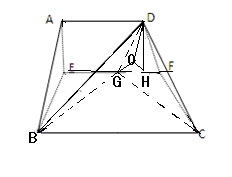
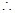 DH
DH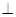 平面EBCF,
平面EBCF,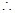 OD
OD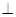 OB,所以
OB,所以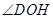 就是所求的二面角
就是所求的二面角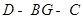 的平面角.由于HG=1,在
的平面角.由于HG=1,在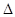 OHG中
OHG中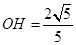 ,
,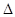 DOH中
DOH中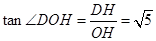
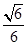


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
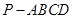 的底面
的底面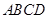 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中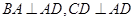 ,
,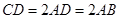 ,平面
,平面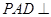 底面
底面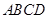 ,
,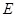 是
是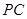 的中点.
的中点.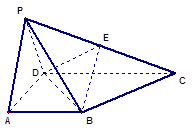
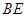 //平面
//平面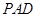 ;
;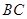 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
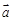 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )| A.4 | B.2 | C.3 | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
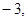 1),点M在
1),点M在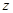 轴上且到A、B两点的距离相等,则M点坐标为
轴上且到A、B两点的距离相等,则M点坐标为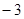 ,0,0)
,0,0)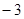 ,0)
,0)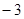 )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com