
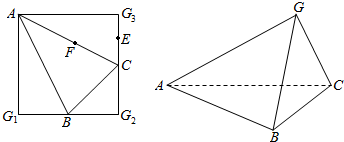
分析 (1)根据折叠前后折痕一侧的角不发生变化可知∠AGB=∠AGC=∠BGC=90°,
(2)根据AG⊥GB,AG⊥GC可得AG⊥平面GBC,故而AG⊥BC;
(3)连结EF,则EF∥AG,故而EF⊥平面GBC,所以平面EFB⊥平面GBC.
解答 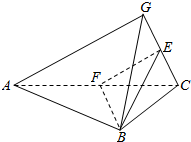 解:(Ⅰ) 在正方形AG1G2G3中,∠G1,∠G2,∠G3都是直角.
解:(Ⅰ) 在正方形AG1G2G3中,∠G1,∠G2,∠G3都是直角.
沿AB,BC及AC把这个正方形折成四面体GABC后,此三个角度数不变.
即在四面体GABC的四个面中,
在△AGB中,∠AGB=90°,
在△AGC中,∠AGC=90°,
在△BGC中,∠BGC=90°,△ABC不是直角三角形.
故分别在平面AGB,平面AGC和平面BGC的三角形是直角三角形.
(Ⅱ)证明:在四面体GABC中,∠AGB=90°,∠AGC=90°,
即AG⊥GB,AG⊥GC,
因为在平面BGC中,GB∩GC=G,
所以,AG⊥平面BGC.
因为BC?平面BGC,
所以,AG⊥BC.
(Ⅲ) 证明:因为在△AGC中,点E,F分别是GC,AC的中点,
所以EF∥AG,
由(Ⅱ)知 AG⊥平面BGC
故EF⊥平面BGC,
因为EF?平面EFB,
所以平面EFB⊥平面GBC.
点评 本题考查了线面垂直的判定与性质,面面垂直的判定,属于中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的值变化很小 | B. | 函数f(x)的值变化很大 | ||
| C. | 函数f(x)的值不变化 | D. | 当n很大时,函数f(x)的值变化很小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
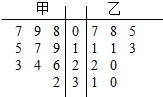 某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )
某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,5] | B. | (-∞,-1]∪[5,+∞) | C. | [-1,+∞) | D. | (-∞,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com