练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若x∈R，n∈N，定义Mxn=x（x+1）（x+2）…（x+n-1），例如，M-43=（-4）（-3）（-2）=-24，则函数f（x）=Mx-511•sinx的奇偶性是（　　）
    A．是偶函数不是奇函数B．是奇函数不是偶函数
    C．既是奇函数又是偶函数D．既不是奇函数也不是偶函数

    分析 由新定义写出函数f（x）的解析式，然后利用函数奇偶性的定义判断．

    解答 解：由定义可知，f（x）=Mx-511•sinx=（x-5）（x-4）（x-3）…（x+5）sinx
    =（x2-25）（x2-16）（x2-9）（x2-4）（x2-1）x•sinx．
    ∵定义域为R，且f（-x）=（x2-25）（x2-16）（x2-9）（x2-4）（x2-1）（-x）•sin（-x）
    =（x2-25）（x2-16）（x2-9）（x2-4）（x2-1）x•sinx=f（x）．
    ∴函数f（x）=Mx-511•sinx是偶函数不是奇函数．
    故选：A．

    点评 本题是新定义题，考查函数奇偶性的判断，属基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

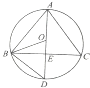    10．如图所示，D为△ABC的外接圆$\widehat{BC}$的中点，点O在AD上，且OD=BD，AD与BC相交于E．
    （I）证明；AD，OD，DE三条线段长成等比数列；
    （Ⅱ）若点O到AB的距离为2，试求△ABC的内切圆的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．（1）已知sinα=$\frac{12}{13}$，并且α是第二象限角，求cosα，tanα，cotα
    （2）已知cosα=-$\frac{4}{5}$，求sinα，tanα

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

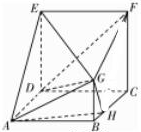    8．在多面体ABCDEFG中，四边形ABCD与CDEF均为正方形，CF⊥平面ABCD，BG⊥平面ABCD，且AB=2BG=4BH．
    （Ⅰ）求证：GH⊥平面EFG；
    （Ⅱ）求二面角D-FG-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．双曲线3x2-y2=75上一点P到它的一个焦点距离等于12，那么点P到它的另一个焦点的距离等于（　　）
    A．2或22B．22C．2D．7或17

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．过双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}$=1左焦点F1的直线交曲线的左支于M，N两点，F2为其右焦点，则|MF2|+|NF2|-|MN|的值为12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．设A={x|-1＜x＜2}，B={x|0＜x＜3}，则A∪B=（-1，3）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设集合A={x|a≤x≤a+3}，集合B={x|x2-4x-5＞0}，分别就下列条件求实数a的取值范围：
    （1）A∩B≠∅，
    （2）A∩B=A．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．满足{1，2，3}⊆A?{1，2，3，4，5，6}的集合A的个数为7．

    查看答案和解析>>

    同步练习册答案