
分析 (1)利用同角三角函数的基本关系,以及三角函数在各个象限中的符号,求得要求式子的值.
(2)分类讨论,利用同角三角函数的基本关系,求得sinα,tanα的值.
解答 解:(1)∵sinα=$\frac{12}{13}$,并且α是第二象限角,
∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{5}{13}$,tanα=$\frac{sinα}{cosα}$=-$\frac{12}{5}$,cotα=$\frac{1}{tanα}$=-$\frac{5}{12}$.
(2)已知cosα=-$\frac{4}{5}$,∴α是第二或第三象限角.
若α是第二象限角,则sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$;
若α是第三象限角,则sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{3}{5}$,tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
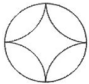 把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为$\frac{4}{π}-1$.
把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为$\frac{4}{π}-1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是偶函数不是奇函数 | B. | 是奇函数不是偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数也不是偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com