
分析 (1)设Q(x0,4),代入抛物线方程,结合抛物线的定义,可得p=2,进而得到抛物线方程;
(2)设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),B(x2,y2)根据韦达定理可求得x1x2的值,又根据抛物线定义可知|AF|=x1+1,|BF|=x2+1代入$\frac{1}{|AF|}+\frac{1}{|BF|}$可得其值.
解答 解:(1)设Q(x0,4),代入由y2=2px(p>0)中得x0=$\frac{8}{p}$,
所以|PQ|=$\frac{8}{p}$,|QF|=$\frac{p}{2}$+$\frac{8}{p}$,
由题设得$\frac{p}{2}$+$\frac{8}{p}$=$\frac{5}{4}$×$\frac{8}{p}$,解得p=-2(舍去)或p=2.
所以C的方程为y2=4x.
(2)易知F坐标(1,0),设过F点直线方程为y=k(x-1)
代入抛物线方程,得 k2(x-1)2=4x.
化简后为:k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2)
则有x1x2=1
根据抛物线性质可知,|AF|=x1+1,|BF|=x2+1
∴$\frac{1}{|AF|}+\frac{1}{|BF|}$=$\frac{{x}_{1}+1+{x}_{2}+1}{({x}_{1}+1)({x}_{2}+1)}$=$\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}+{x}_{2}+2}$=1.
点评 本题主要考查抛物线的应用和抛物线定义.对于过抛物线焦点的直线与抛物线关系,常用抛物线的定义来解决.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
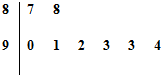 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91、5 | B. | 91、5.5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,+∞) | B. | [-1,0)∪(0,+∞) | C. | (-1,+∞) | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | -$\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com