
分析 分别对g(x),h(x),ϕ(x)求导,令g′(x)=g(x),h′(x)=h(x),ϕ′(x)=ϕ(x),则它们的根分别为α,β,γ,然后分别讨论α,β,γ的取值范围即可.
解答 解:∵g′(x)=1,h′(x)=$\frac{2}{x}$,ϕ′(x)=3x2,
由g(x)=g′(x)得x=1,即
α=1,
由h(x)=h′(x),
得2lnx=$\frac{2}{x}$,即lnx-$\frac{1}{x}$=0,
设m(x)=lnx-$\frac{1}{x}$,在(0,+∞)上函数m(x)为增函数,
∵m(1)=0-1<0,m(2)=ln2-$\frac{1}{2}$>0,
∴1<β<2;
由ϕ(x)=ϕ′(x)得
x3-1=3x2,
即x3-3x2-1=0,
设q(x)=x3-3x2-1,
则q′(x)=3x2-6x=3x(x-2),
由q′(x)>0得x>2或x<0,此时函数单调递增,
由q′(x)<0得0<x<2,此时函数单调递递减,
当x=0时,函数取得极大值q(0)=-1<0,
∵q(3)=33-3×32-1=-1<0,
∴函数q(x)=x3-3x2-1的零点γ>3,
∴γ>β>α.
故答案为 γ>β>α
点评 本题主要考查函数零点的大小比较,求函数的导数,建立方程关系,分别判断论α,β,γ的取值范围是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}⊥\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|>|$\overrightarrow{b}$| | C. | θ∈(0,$\frac{π}{2}$) | D. | $θ∈(\frac{π}{2},π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
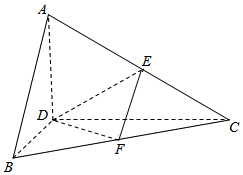 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b∈R,且a+b>4,则a,b至少有一个大于2 | |
| B. | “?x0∈R,${2^{x_0}}=1$”的否定是“?x∈R,2x≠1” | |
| C. | a>1,b>1是ab>1的必要条件 | |
| D. | △ABC中,A是最大角,则sin2A>sin2B+sin2C是△ABC为钝角三角形的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com