选修4－4：坐标系与参数方程选讲．
在直角坐标系xOy中，曲线C1的参数方程为
（α是参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝
.
（1）求曲线C1的普通方程和曲线C2的直角坐标方程；
（2）求曲线C1上的任意一点P到曲线C2的最小距离，并求出此时点P的坐标.
科目：高中数学 来源：2015-2016学年辽宁鞍山一中等校高二下期末理科数学试卷（解析版） 题型：选择题
有一段“三段论”推理是这样的：对于定义域内可导函数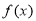
，如果
，那么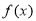
在定义域内单调递增；因为函数
满足在定义域内导数值恒正，所以，
在定义域内单调递增.以上推理中（ ）
A．大前提错误 B．小前提错误 C．推理形式错误 D．结论正确
查看答案和解析>>
科目：高中数学 来源：2017届广州省惠州市高三第一次调研理科数学试卷（解析版） 题型：选择题
双曲线
实轴的两个顶点为
，点
为双曲线
上除
外的一个动点，若
，则动点
的运动轨迹为（ ）
A．圆 B．椭圆 C．双曲线 D．抛物线
查看答案和解析>>
科目：高中数学 来源：2017届广州省惠州市高三第一次调研理科数学试卷（解析版） 题型：选择题
将函数
图象上各点横坐标伸长到原来的2倍，再向左平移
个单位，所得函数图象的解析式是（ ）
A．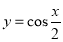
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2017届湖南师大附中高三上入学摸底文科数学试卷（解析版） 题型：解答题
某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如下图．
（1）求分数在[50，60）的频率及全班人数；
（2）求分数在[80，90）之间的频数，并计算频率分布直方图中[80，90）间矩形的高；
（3）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在[90，100）之间的概率．
查看答案和解析>>
科目：高中数学 来源：2017届湖南师大附中高三上入学摸底文科数学试卷（解析版） 题型：选择题
如图，已知正三棱柱ABC－A1B1C1的各条棱长都相等，则异面直线AB1和A1C所成的角的余弦值大小为
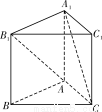
A. 
B．－ C．
D．－
查看答案和解析>>
科目：高中数学 来源：2017届湖南师大附中高三上入学摸底理科数学试卷（解析版） 题型：解答题
空气质量指数（Air Quality Index，简称AQI）是定量描述空气质量状况的指数， 空气质量按照AQI大小分为六级：0～50为优；51～100为良；101～150为轻度污染；151～200为中度污染；201～300为重度污染；＞300为严重污染．
一环保人士记录去年某地某月10天的AQI的茎叶图如下．
（1）利用该样本估计该地本月空气质量优良（AQI≤100）的天数；（按这个月总共30天计算）
（2）将频率视为概率，从本月中随机抽取3天，记空气质量优良的天数为ξ，求ξ的概率分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年河北省高二下期中理科数学试卷（解析版） 题型：解答题
将一个半径适当的小球放入如图所示的容器最上方的入口处，小球自由下落，小球在下落的过程中，将遇到黑色障碍物3次，最后落入A袋或B袋中．已知小球每次遇到障碍物时，向左、右两边下落的概率分别是
（1）分别求出小球落入A袋和B袋中的概率；
（2）在容器的入口处依次放入4个小球，记ξ为落入B袋中的小球个数，求ξ的分布列和数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
，
，
.
.
，求角
；
，求
.