练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．化简$\frac{1}{{cos{{20}°}}}-\frac{{\sqrt{3}}}{{sin{{20}°}}}$=-4．

    分析 对已知通分，逆用两角和与差的三角函数公式以及正弦的倍角公式化简．

    解答 解：$\frac{1}{{cos{{20}°}}}-\frac{{\sqrt{3}}}{{sin{{20}°}}}$=$\frac{sin20°-\sqrt{3}cos20°}{cos20°sin20°}$=$\frac{2sin（20°-60°）}{\frac{1}{2}sin40°}=\frac{-2sin40°}{\frac{1}{2}sin40°}$=-4．
    故答案为：-4．

    点评 本题考查了三角函数式的化简求值；利用了两角和与差的三角函数公式以及正弦的倍角公式；属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．|a-b|=|a|+|b|成立的条件是（　　）
    A．ab＞0B．ab＞1C．ab≤0D．ab≤1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．不等式$\frac{x-1}{x+2}$＞0的解集是{x|x＞1或x＜-2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某产品生产厂家根据以往的生产销售经验得到下面有关销售的统计规律：每生产产品x（百台），其总成本为G（x）万元，其中固定成本为2万元，并且每生产100台的生产成本为1万元（总成本=固定成本+生产成本），销售收入R（x）满足R（x）=$\left\{\begin{array}{l}{-0.4{x}^{2}+4.2x-0.8（0≤x≤5）}\\{10.2（x＞5）}\end{array}\right.$，假定该产品产销平衡，那么根据上述统计规律：
    （1）要使工厂有盈利，产品数量x应控制在什么范围？
    （2）工厂生产多少台产品时盈利最大？此时每台产品售价为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在△ABC中，若lna-lncosB=lnb-lncosA，其中角A，B的对边分别为a，b，则△ABC的形状为（　　）
    A．等腰三角形B．直角三角形
    C．等边三角形D．等腰或直角三角形

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

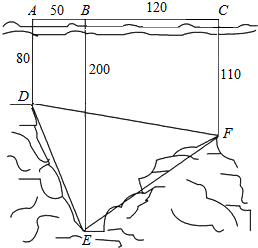    10．马航MH370牵动全球人的心，世界各国积极投身到马航的搜救工作中，了解海底构造是救援工作要做的第一件事．某搜救队在某海域的海平面上的同一条直线上的A，B，C三点进行测量，得AB=50，BC=120，于A，B，C三处测得水深分别为AD=80，BE=200，CF=110，如图所示，试利用你所学知识求∠DEF的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

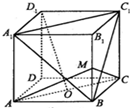
    17．如图，正方体ABCD-A1B1C1D1中，O为底面ABCD的中心，M为棱BB1的中点，则下列结论中错误的是（　　）
    A．D1O∥平面A1BC1B．D1O⊥平面AMC
    C．二面角M-AC-B等于45°D．异面直线BC1与AC所成的角等于60°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．为调查某社区居民的业余生活状况，研究这一社区居民在20：00-22：00时间段的休闲方式与性别的关系，随机调查了该社区80人，得到下面的数据表：
    休闲方式
    性别    		看电视看书合计
    男105060
    女101020
    合计206080
    （Ⅰ）根据以上数据，能否有99%的把握认为“在20：00-22：00时间段居民的休闲方式与性别有关系”？
    （Ⅱ）将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X．求X的数学期望和方差．
    P（X2≥k）0.0500.0100.001
    k3.8416.63510.828
    附：X2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+n+{1}^{n}+2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．函数y=lnx-x的递增区间是（0，1]．

    查看答案和解析>>

    同步练习册答案