
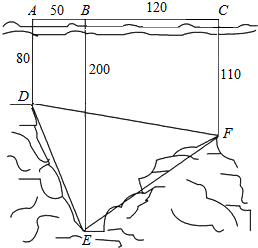
 马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值.
马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值. 分析 先利用勾股定理分别求得DF,DE和EF,进而利用余弦定理求得cos∠DEF的值.
解答 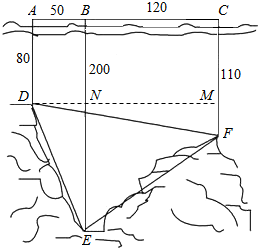 解:如图作DM∥AC交BE于N,交CF于M.
解:如图作DM∥AC交BE于N,交CF于M.
DF=$\sqrt{M{F}^{2}+D{M}^{2}}$=10$\sqrt{298}$(m),
DE$\sqrt{D{N}^{2}+E{N}^{2}}$=130(m),
EF=$\sqrt{(BE-FC)^{2}+B{C}^{2}}$150(m).
在△DEF中,由余弦定理的变形公式,得
cos∠DEF=$\frac{13{0}^{2}+15{0}^{2}-1{0}^{2}×298}{2130×150}$=$\frac{16}{65}$.
点评 本题主要考查了解三角形问题的实际应用.综合考查了三角形问题中勾股定理,余弦定理的灵活运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 243 | B. | 729 | C. | 1024 | D. | 4096 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com