
分析 (1)利用两角和公式和二倍角公式求得cosC的值.
(2)设出BC,则AB,AC,AM,CM可知,利用余弦定理求得BM,进而利用正弦定理求得sin∠CBM,则cot∠CBM可求得,最后利用诱导公式求得答案.
解答 解:(1)8sin2($\frac{A+B}{2}$)+3cos2C=8•$\frac{1-cos(A+B)}{2}$+3cos2C=4-4cos(A+B)+3cos2C=4+4cosC+3cos2C=3,
∴3cos2C+4cosC+1=0,
∴6cos2C+4cosC-2=0,
∴cosC=-1或$\frac{1}{3}$,
故cos=$\frac{1}{3}$.
(2)如图:B=$\frac{π}{2}$,cosC=$\frac{1}{3}$,
做MN∥BC,交AB于点N,
设BC=t,则AC=3t,AM=t,CM=2t,AB=2$\sqrt{2}$t,
又由MN∥BC,
则MN=$\frac{1}{3}$BC=$\frac{t}{3}$,NB=$\frac{2}{3}$AB=$\frac{4\sqrt{2}}{3}$t,
tan∠ABM=$\frac{MN}{NB}$=4$\sqrt{2}$.
点评 本题主要考查了正弦定理和余弦定理的运用.解题过程中运用了转化的思想,求得cosC的值是关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 39 | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
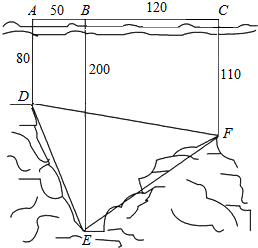 马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值.
马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com