
| A. | 19 | B. | 39 | C. | 10 | D. | 20 |
分析 由等差数列的性质和已知可得am=1,再由求和公式和性质可得S2m-1=$\frac{(2m-1)({a}_{1}+{a}_{2m-1})}{2}$=(2m-1)am=39,代值解关于m的方程可得.
解答 解:∵am-1+am+1-am-1=0,
∴由等差数列的性质可得am-1+am+1=2am,
代入上式可得2am-am-1=0,解得am=1,
∴S2m-1=$\frac{(2m-1)({a}_{1}+{a}_{2m-1})}{2}$=39,
∴$\frac{(2m-1)×2{a}_{m}}{2}$=(2m-1)am=39,
∴2m-1=39,解得m=20
故选:D
点评 本题考查等差数列的求和公式和性质,属基础题.


科目:高中数学 来源: 题型:解答题
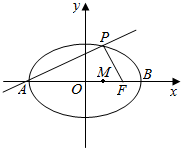 如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.
如图所示,点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF,设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 243 | B. | 729 | C. | 1024 | D. | 4096 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 20 | C. | 25 | D. | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com