
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
���� ��ȡ����{an}Ϊ�����У������Ƴ��������Ǽ����⣻
�ڸ��ݵȲ����е����ʣ��Ƴ�2��S2n-Sn��=Sn+��S3n-S2n�������ɵõ�Sn��S2n-Sn��S3n-S2n����Ϊ�Ȳ����У�
�����õȱ����е������ж�ѡ���Ƿ���ȷ��
�ܸ������е�ǰn��ĺͼ�ȥ��n-1��ĺ͵õ����еĵ�n���ͨ�ʽ�����ɵõ��˵ȱ����е������빫�ȣ�����������ȣ����õȱ����е�ǰn��͵Ĺ�ʽ��ʾ��ǰn��ĺͣ���ϵȱ�����ǰn���ʽ�����ɵý����Ƿ���ȷ��
��� �⣺��ȡ����{an}Ϊ�����У�������m��n��s��t��N*������am+an=as+at���ʴ���
����Ȳ�����an������Ϊa1������Ϊd��
��Sn=a1+a2+��+an��S2n-Sn=an+1+an+2+��+a2n=a1+nd+a2+nd+��+an+nd=Sn+n2d��
ͬ����S3n-S2n=a2n+1+a2n+2+��+a3n=an+1+an+2+��+a2n+n2d=S2n-Sn+n2d��
��2��S2n-Sn��=Sn+��S3n-S2n����
��Sn��S2n-Sn��S3n-S2n�ǵȲ����У���ѡ����ȷ��
����an=��-1��n��
��S2=0��S4-S2=0��S6-S4=0��
������в��ǵȱ����У���ѡ�����
����Ϊan=Sn-Sn-1=��Aqn+B��-��Aqn-1+B��=Aqn-Aqn-1=��Aq-1��•qn-1��
���Դ�����Ϊ������Aq-1������Ϊq�ĵȱ����У�
��Sn=$\frac{��Aq-1����1-{q}^{n}��}{1-q}$��
����B=$\frac{Aq-1}{1-q}$��A=-$\frac{Aq-1}{1-q}$����A+B=0������ȷ��
���Тڢ���ȷ��
��ѡ��C��
���� ���⿼��ѧ��������õȲ�ȱ����е����ʻ�����ֵ����һ���ۺ��⣮���е��⣮


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
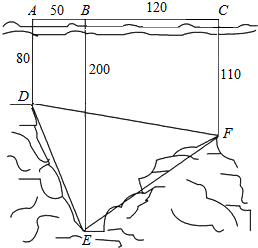 ����MH370ǣ��ȫ���˵��ģ������������Ͷ�����������Ѿȹ����У��˽⺣�����Ǿ�Ԯ����Ҫ���ĵ�һ���£�ij�Ѿȶ���ij����ĺ�ƽ���ϵ�ͬһ��ֱ���ϵ�A��B��C������в�������AB=50��BC=120����A��B��C�������ˮ��ֱ�ΪAD=80��BE=200��CF=110����ͼ��ʾ������������ѧ֪ʶ���DEF������ֵ��
����MH370ǣ��ȫ���˵��ģ������������Ͷ�����������Ѿȹ����У��˽⺣�����Ǿ�Ԯ����Ҫ���ĵ�һ���£�ij�Ѿȶ���ij����ĺ�ƽ���ϵ�ͬһ��ֱ���ϵ�A��B��C������в�������AB=50��BC=120����A��B��C�������ˮ��ֱ�ΪAD=80��BE=200��CF=110����ͼ��ʾ������������ѧ֪ʶ���DEF������ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ҫ���� | B�� | ��ַDZ�Ҫ���� | ||
| C�� | ��Ҫ�dz������ | D�� | �ȷdz���ַDZ�Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
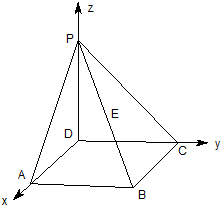 PD��ֱ��������ABCD����ƽ�棬AB=2��EΪPB���е㣬cos��$\overrightarrow{DP}$��$\overrightarrow{AE}$��=$\frac{\sqrt{3}}{3}$��������ͼ��ʾ�����ռ�ֱ������ϵ����E������Ϊ��������
PD��ֱ��������ABCD����ƽ�棬AB=2��EΪPB���е㣬cos��$\overrightarrow{DP}$��$\overrightarrow{AE}$��=$\frac{\sqrt{3}}{3}$��������ͼ��ʾ�����ռ�ֱ������ϵ����E������Ϊ��������| A�� | ��1��1��2�� | B�� | ��2��2��1�� | C�� | ��1��1��1�� | D�� | $��1\;��\;1\;��\;\frac{1}{2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 60���120�� | C�� | 30�� | D�� | 30���150�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com