
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\frac{2\sqrt{10}}{5}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 求出双曲线的渐近线方程,设两条渐近线的夹角为θ,由两直线的夹角公式,可得tanθ=tan∠MON,求出F到渐近线y=$\frac{b}{a}$x的距离为b,即有|ON|=a,△OMN的面积可以表示为$\frac{1}{2}$•a•atanθ,结合条件可得a,b的关系,再由离心率公式即可计算得到.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{b}{a}$x,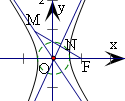
设两条渐近线的夹角为θ,
则tanθ=tan∠MON=$\frac{\frac{b}{a}-(-\frac{b}{a})}{1+\frac{b}{a}•(-\frac{b}{a})}$=$\frac{2ab}{{a}^{2}-{b}^{2}}$,
设FN⊥ON,则F到渐近线y=$\frac{b}{a}$x的距离为d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
即有|ON|=$\sqrt{{c}^{2}-{b}^{2}}$=a,
则△OMN的面积可以表示为$\frac{1}{2}$•a•atanθ=$\frac{{a}^{3}b}{{a}^{2}-{b}^{2}}$=$\frac{3{a}^{2}}{8}$,
解得a=3b,
则e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{1}{9}}$=$\frac{\sqrt{10}}{3}$.
故选:B.
点评 本题考查双曲线的方程和性质,主要考查离心率的求法,同时考查两直线的夹角公式和三角形的面积公式,结合着较大的运算量,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:选择题
 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
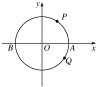 如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.
如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的周期为π,且在区间[$\frac{π}{3}$,π]内单调递增 | |
| B. | 函数f(x)的周期为π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| C. | 函数f(x)的周期为2π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| D. | 函数f(x)的周期为$\frac{π}{2}$,且在区间[$\frac{π}{2}$,π]内单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com