
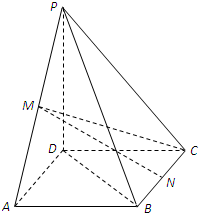
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别是PA,PB的中点,PD⊥平面ABCD,且PD=AD=| 2 |
| MC |
| BD |
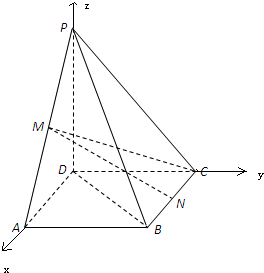 (Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)
(Ⅰ)证明:取AD中点E,连结ME,NE,…(2分)| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| BD |
| 2 |
| MC |
| ||
| 2 |
| ||
| 2 |
| MC |
| BD |


科目:高中数学 来源:2014-2015学年江西省赣州市北校高二1月月考文科数学试卷(解析版) 题型:选择题
如图,正方体 的棱长为
的棱长为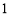 ,点
,点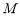 在棱
在棱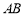 上,且
上,且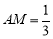 ,点
,点 是平面
是平面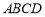 上的动点,且动点
上的动点,且动点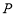 到直线
到直线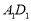 的距离与点
的距离与点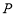 到点
到点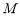 的距离的平方差为
的距离的平方差为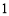 ,则动点
,则动点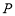 的轨迹是 ( )
的轨迹是 ( )

A.圆 B.抛物线 C.双曲线 D.椭圆
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市北校高二1月月考文科数学试卷(解析版) 题型:选择题
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
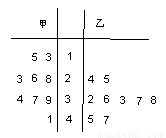
A.62 B.63 C.64 D.56
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ON |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com