
【题目】已知函数![]() 是偶函数,
是偶函数, ![]() (其中
(其中![]() ).
).
(1)求函数![]() 的定义域;
的定义域;
(2)求![]() 的值;
的值;
(3)若函数![]() 与
与![]() 的图象有且只有一个交点,求
的图象有且只有一个交点,求![]() 的取值范围.
的取值范围.
【答案】(1)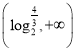 (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据对数函数的性质有![]() 解不等式即可求出函数的定义域;
解不等式即可求出函数的定义域;
(2)函数![]() 是偶函数,所以
是偶函数,所以![]() =
= ![]() ,即有
,即有![]() 由此可求出k的值;
由此可求出k的值;
(3)函数![]() 与
与![]() 的图象有且只有一个交点,即方程
的图象有且只有一个交点,即方程![]() 在
在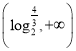 上只有一解,令
上只有一解,令![]() 则
则![]() ,问题转化为关于t的方程(a-1)t2-
,问题转化为关于t的方程(a-1)t2-![]() 在(
在(![]() ,
, ![]() 上只有一解,分
上只有一解,分![]() 三种情况进行讨论即可求得
三种情况进行讨论即可求得![]() 的取值范围.
的取值范围.
试题解析:
(1)∵![]() ,且
,且![]()
∴![]()
∴![]()
所以![]() 定义域为
定义域为![]()
(2)∵是偶函数
∴![]() 对任意
对任意![]() 恒成立
恒成立
即![]() 恒成立,
恒成立,
∴![]()
(3)∵函数![]() 与
与![]() 的图象有且只有一个交点
的图象有且只有一个交点
∴方程![]() 在
在![]() 上只有一解
上只有一解
即方程![]() 在
在![]() 上只有解
上只有解
令![]() 则
则![]()
因而等价于关于![]() 的方程
的方程![]() 在
在![]() 上只有一个解
上只有一个解
①当![]() 时,解得
时,解得![]() ,不合题意
,不合题意
②当0<a<1时,记h(t)=(a﹣1)t2﹣![]() at﹣1,
at﹣1,
其图象的对称轴t=![]() <0,
<0,
∴函数h(t)在(0,+∞)上递减,而h(0)=﹣1,
∴方程![]() 在(
在(![]() ,+∞)无解;
,+∞)无解;
③当a>1时,记h(t)=(a﹣1)t2﹣![]() at﹣1,
at﹣1,
其图象的对称轴t=![]() >0,h(0)=﹣1,
>0,h(0)=﹣1,
所以,只需h(![]() )<0,即
)<0,即![]() (a﹣1)﹣
(a﹣1)﹣![]() a﹣1<0,此恒成立,
a﹣1<0,此恒成立,
∴此时a的范围为a>1,
综上所述,所求a的取值范围为a>1.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务,某市移动公司欲提供新的资费套餐(资费包含手机月租费、手机拨打电话费与家庭宽带上网费)。其中一组套餐变更如下:
原方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
18元/月 | 0.2元/分钟 | 50元/月 |
新方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
58元/月 | 前100分钟免费, 超过部分 | 免费 |
(1)客户甲(只有一个手机号和一个家庭宽带上网号)欲从原方案改成新方案,设其每月手机通话时间为![]() 分钟(
分钟(![]() ),费用
),费用![]() 原方案每月资费-新方案每月资费,写出
原方案每月资费-新方案每月资费,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)经过统计,移动公司发现,选这组套餐的客户平均月通话时间![]() 分钟,为能起到降费作用,求
分钟,为能起到降费作用,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上且满足下列两个条件:
上且满足下列两个条件:
①对任意![]() 都有
都有![]() ;
;
②当![]() 时,有
时,有![]() ,
,
(1)求![]() ,并证明函数
,并证明函数![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(3)若![]() ,试求函数
,试求函数![]() 的零点.
的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:经过定点P0(x0 , y0)的直线都可以用方程y﹣y0=k(x﹣x0)表示,命题q:直线xtan ![]() +y﹣7=0的倾斜角是
+y﹣7=0的倾斜角是 ![]() ,则下列命题是真命题的为( )
,则下列命题是真命题的为( )
A.(p)∧q
B.p∧q
C.p∨(q)
D.(P)∧(q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的两个焦点是F1、F2 , 过F1的直线与椭圆C交于P、Q,若|PF2|=|F1F2|,且5|PF1|=6|F1Q|,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2017年“双11”,“双12”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共100个,生产一个汤碗需5分钟,生产一个花瓶需7分钟,生产一个茶杯需4分钟,已知总生产时间不超过10小时.若生产一个汤碗可获利润5元,生产一个花瓶可获利润6元,生产一个茶杯可获利润3元.
(1)使用每天生产的汤碗个数x与花瓶个数y表示每天的利润ω(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语句p:曲线x2﹣2mx+y2﹣4y+2m+7=0表示圆;语句q:曲线 ![]() +
+ ![]() =1表示焦点在x轴上的椭圆,若p∨q为真命题,¬p为真命题,求实数m的取值范围.
=1表示焦点在x轴上的椭圆,若p∨q为真命题,¬p为真命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com