
【题目】若无穷数列![]() 满足:
满足:![]() 是正实数,当
是正实数,当![]() 时,
时,![]() ,则称
,则称![]() 是“
是“![]() —数列”.
—数列”.
(1)若![]() 是“
是“![]() —数列”且
—数列”且![]() ,写出
,写出![]() 的所有可能值;
的所有可能值;
(2)设![]() 是“
是“![]() —数列”,证明:
—数列”,证明:![]() 是等差数列当且仅当
是等差数列当且仅当![]() 单调递减;
单调递减;![]() 是等比数列当且仅当
是等比数列当且仅当![]() 单调递增;
单调递增;
(3)若![]() 是“
是“![]() —数列”且是周期数列(即存在正整数
—数列”且是周期数列(即存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() ),求集合
),求集合![]() 的元素个数的所有可能值的个数.
的元素个数的所有可能值的个数.
【答案】(1)-2,0,2,8(2)证明见解析(3)当![]() 时,有32种;当
时,有32种;当![]() 时,有31种.
时,有31种.
【解析】
(1)根据“![]() —数列”的定义逐项分析即可.
—数列”的定义逐项分析即可.
(2)分别根据等差等比数列的定义,分别证明对应的必要性和充分性即可.
(3)分别证明![]() 是数列
是数列![]() 中的最大项与当
中的最大项与当![]() 是奇数时,
是奇数时,![]() 是
是![]() 的奇数倍;当
的奇数倍;当![]() 是偶数时,
是偶数时,![]() 是
是![]() 的偶数倍再根据周期的性质证明即可.
的偶数倍再根据周期的性质证明即可.
(1)解:由题,所有可能的情况有![]() ,
,![]() ,
,![]() .
.
故![]() 的所有可能值为 -2,0,2,8.
的所有可能值为 -2,0,2,8.
(2)证明:因为![]() ,所以
,所以![]() 或
或![]() .
.
当![]() 是等差数列时,假设
是等差数列时,假设![]() ,则
,则![]() ,此时,
,此时,![]() ,而
,而![]() ,矛盾!所以
,矛盾!所以![]() .于是公差
.于是公差![]() ,所以
,所以![]() 单调递减.
单调递减.
当![]() 单调递减时,对任意
单调递减时,对任意![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() ,从而
,从而![]() 是等差数列.
是等差数列.
当![]() 是等比数列时,
是等比数列时,![]() ,所以
,所以![]() ,于是公比
,于是公比![]() .又
.又![]() ,所以
,所以![]() 单调递增.
单调递增.
当![]() 单调递增时,对任意
单调递增时,对任意![]() ,
,![]() .又
.又![]() ,所以
,所以![]() ,即
,即![]() .因为
.因为![]() ,所以
,所以![]() 是等比数列.
是等比数列.
(3)解:先证明![]() 是数列
是数列![]() 中的最大项.
中的最大项.
事实上,如果![]() 是第一个大于
是第一个大于![]() 的项的脚标,则由
的项的脚标,则由
![]()
知,![]() 是
是![]() 的倍数.假设
的倍数.假设![]() ,
,![]() ,…,
,…,![]() 都是
都是![]() 的倍数,则由
的倍数,则由
![]()
![]()
知,![]() 也是
也是![]() 的倍数.所以由归纳法知,对任意
的倍数.所以由归纳法知,对任意![]() ,
,![]() 都是
都是![]() 的倍数,但
的倍数,但![]() 不是
不是![]() 的倍数,这与
的倍数,这与![]() 是周期数列矛盾!
是周期数列矛盾!
所以![]() 是数列
是数列![]() 中的最大项,从而当
中的最大项,从而当![]() 时,
时,![]() .
.
再证明当![]() 是奇数时,
是奇数时,![]() 是
是![]() 的奇数倍;当
的奇数倍;当![]() 是偶数时,
是偶数时,![]() 是
是![]() 的偶数倍.
的偶数倍.
事实上,当![]() 时结论成立.假设
时结论成立.假设![]() 时成立,当
时成立,当![]() 时,由
时,由![]() 知,结论也成立.
知,结论也成立.
设![]() 的最小正周期是
的最小正周期是![]() ,因为
,因为![]() ,所以
,所以![]() 是偶数.
是偶数.
反过来,当![]() 是偶数时,我们证明存在一个以
是偶数时,我们证明存在一个以![]() 为最小正周期的“
为最小正周期的“![]() 一数列”
一数列”![]() .
.
事实上,令![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,之后再以
,之后再以![]() 为周期循环即可.
为周期循环即可.
当![]() 以
以![]() 为最小正周期时,集合
为最小正周期时,集合![]() 的元素个数为
的元素个数为![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数.因此所求即为
的最大整数.因此所求即为![]() ,
,![]() ,…,
,…,![]() 中不同项的个数.
中不同项的个数.
当![]() 时,
时,![]() ,所以从
,所以从![]() 到0中的所有整数值都能取到,有32种.
到0中的所有整数值都能取到,有32种.
当![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() ,…,
,…,![]() 两两不同,有31种.
两两不同,有31种.


科目:高中数学 来源: 题型:
【题目】两个三口之家,共![]() 个大人,
个大人,![]() 个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐
个小孩,约定星期日乘红色、白色两辆轿车结伴郊游,每辆车最多乘坐![]() 人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
人,其中两个小孩不能独坐一辆车,则不同的乘车方法种数是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网购逐步走入百姓生活,网络(电子)支付方面的股票受到一些股民的青睐.某单位4位热爱炒股的好朋友研究后决定购买“生意宝”和“九州通“这两支股票中的一支.他们约定:每人通过掷一枚质地均匀的骰子决定购买哪支股票,掷出点数为5或6的人买“九州通”股票,掷出点数为小于5的人买“生意宝”股票,且必须从“生意宝”和“九州通”这两支股票中选择一支股票购买.
(1)求这4人中恰有1人购买“九州通”股票的機率;
(2)用![]() ,
,![]() 分别表示这4人中购买“生意宝”和“九州通”股票的人数,记
分别表示这4人中购买“生意宝”和“九州通”股票的人数,记![]() ,求随机变量X的分布列与数学期望
,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处取得最大值,求实数
处取得最大值,求实数![]() 的值;
的值;
(2)若![]() ,求
,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若![]() ,直线
,直线![]() 都不是曲线
都不是曲线![]() 的切线,求
的切线,求![]() 的取值范围(只需直接写出结果).
的取值范围(只需直接写出结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高山滑雪运动的曲道赛项目中,运动员从高处(起点)向下滑,在滑行中运动员要穿过多个高约0.75米,宽4至6米的旗门,规定:运动员不经过任何一个旗门,都会被判一次“失格”,滑行时间会被增加,而所用时间越少,则排名越高.已知在参加比赛的运动员中,有五位运动员在滑行过程中都有三次“失格”,其中
(1)甲在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(2)乙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(3)丙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(4)丁在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(5)戊在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门.
三个旗门.
根据以上信息,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这8个旗门从上至下的排列顺序共有( )种可能.
这8个旗门从上至下的排列顺序共有( )种可能.
A.6B.7C.8D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,四边形
,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,
,![]() ,E,F分别为AC,
,E,F分别为AC,![]() 的中点.
的中点.

(1)求证:直线EF∥平面![]() ;
;
(2)设![]() 分别在侧棱
分别在侧棱![]() ,
,![]() 上,且
上,且![]() ,求平面BPQ分棱柱所成两部分的体积比.
,求平面BPQ分棱柱所成两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() 如下:对于实数
如下:对于实数![]() ,如果存在整数
,如果存在整数![]() ,使得
,使得![]() ,则
,则![]() .则下列结论:①
.则下列结论:①![]() 是实数
是实数![]() 上的递增函数;②
上的递增函数;②![]() 是周期为1的函数;③
是周期为1的函数;③![]() 是奇函数;④函数
是奇函数;④函数![]() 的图像与直线
的图像与直线![]() 有且仅有一个交点.则正确结论的序号是______.
有且仅有一个交点.则正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网络已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在我市的普及情况,某调查机构进行了有关网购的调查问卷,并从参与调查的市民中随机抽取了男女各100人进行分析,从而得到表(单位:人)
经常网购 | 偶尔或不用网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为我市市民网购与性别有关?
(2)①现从所抽取的女市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从我市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为![]() ,求随机变量
,求随机变量![]() 的数学期望和方差.
的数学期望和方差.
参考公式: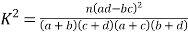
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com