
| A. | p是假命题 | B. | q是真命题 | C. | p∧(¬q)是真命题 | D. | (¬p)∧q是真命题 |
分析 对于命题p:利用指数函数的性质、基本不等式的性质即可判断出真假.对于命题q:当且仅当x0=-1时,${2}^{-1}=\frac{1}{2}$,即可判断出真假.
解答 解:对于命题p:?x∈R,2-x>0,∴${2}^{-x}+\frac{8}{{2}^{-x}}$≥2$\sqrt{{2}^{-x}•\frac{8}{{2}^{-x}}}$=4$\sqrt{2}$,当且仅当x=-$\frac{3}{2}$时取等号.
对于命题q:当且仅当x0=-1时,${2}^{-1}=\frac{1}{2}$,因此q是假命题.
∴只有p∧(¬q)是真命题.
故选:C.
点评 本题考查了基本不等式的性质、函数的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,2} | C. | {x|0≤x≤$\sqrt{3}$} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
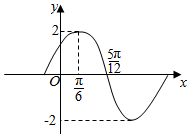 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinA)>f(cosB) | B. | f(sinA)<f(sinB) | C. | f(cosA)<f(cosB) | D. | f(cosA)>f(cosB) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com