
【题目】给出下列四个命题:
①![]() 中,
中,![]() 是
是![]() 成立的充要条件;
成立的充要条件;
②当![]() 时,有
时,有![]() ;
;
③已知![]() 是等差数列
是等差数列![]() 的前n项和,若
的前n项和,若![]() ,则
,则![]() ;
;
④若函数![]() 为
为![]() 上的奇函数,则函数
上的奇函数,则函数![]() 的图象一定关于点
的图象一定关于点![]() 成中心对称.其中所有正确命题的序号为___________.
成中心对称.其中所有正确命题的序号为___________.
【答案】①③
【解析】
①利用正弦定理可判断;②举反例即可判断;③利用等差数列等差中项计算可判断;
④根据奇函数的性质与函数图象平移可判断.
①在△ABC中,由正弦定理可得 ![]() , ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要条件,①正确;
, ∴sinA>sinBa>bA>B,因此A>B是sinA>sinB的充要条件,①正确;
②当1>x>0时,lnx<0,所以不一定大于等于2,②不成立;
③等差数列{an}的前n项和,若S7>S5,则S7-S5=a6+a7>0,S9-S3=a4+a5+…+a9=3(a6+a7)>0,因此S9>S3,③正确;
④若函数![]() 为R上的奇函数,则其图象关于(0,0)中心对称,而函数y=f(x)的图象是把y=f(x-
为R上的奇函数,则其图象关于(0,0)中心对称,而函数y=f(x)的图象是把y=f(x-![]() )的图象向左平移
)的图象向左平移![]() 个单位得到的,故函数y=f(x)的图象一定关于点F(-
个单位得到的,故函数y=f(x)的图象一定关于点F(-![]() ,0)成中心对称,④不正确.
,0)成中心对称,④不正确.
综上只有①③正确.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下:
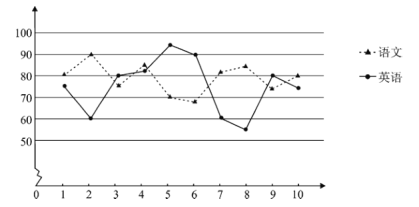
(1)若第二段抽取的学生编号是026,写出第六段抽取的学生编号;
(2)在这两科成绩差低于20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(3)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出至少两条统计结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
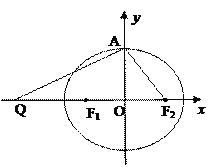
【题目】如图,设椭圆![]() 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且![]() 0,若过 A,Q,F2三点的圆恰好与直线
0,若过 A,Q,F2三点的圆恰好与直线![]() 相切,过定点 M(0,2)的直线
相切,过定点 M(0,2)的直线![]() 与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线
与椭圆C交于G,H两点(点G在点M,H之间).(Ⅰ)求椭圆C的方程;(Ⅱ)设直线![]() 的斜率
的斜率![]() ,在x轴上是否存在点P(
,在x轴上是否存在点P(![]() ,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出
,0),使得以PG,PH为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,请说明理由;(Ⅲ)若实数
的取值范围;如果不存在,请说明理由;(Ⅲ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古印度“汉诺塔问题”:一块黄铜平板上装着![]() 三根金铜石细柱,其中细柱
三根金铜石细柱,其中细柱![]() 上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若
上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若![]() 柱上现有
柱上现有![]() 个金盘(如图),将
个金盘(如图),将![]() 柱上的金盘全部移到
柱上的金盘全部移到![]() 柱上,至少需要移动次数为( )
柱上,至少需要移动次数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
已知曲线C![]() :
:![]() (t为参数), C
(t为参数), C![]() :
:![]() (
(![]() 为参数)。
为参数)。
(1)化C![]() ,C
,C![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为C
,Q为C![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线
![]() (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重100克,次品重110 克.现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品),如果将5袋产品以1-5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() =1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
=1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() =__________克;若次品所在袋子的编号是
=__________克;若次品所在袋子的编号是![]() ,此时的重量
,此时的重量![]() =_________克.
=_________克.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com