
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 8 |
分析 (a-m)2+(b-n)2的几何意义是y=-x2+3lnx的图象上的点与y=x+2的图象上的点的距离的平方;从而求导,求出切线,求平行线间的距离即可.
解答 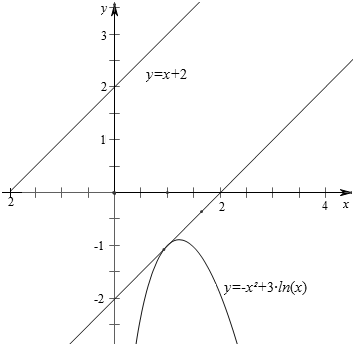 解:∵点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,
解:∵点A(a,b)在y=-x2+3lnx的图象上,点B(m,n)在y=x+2的图象上,
又∵(a-m)2+(b-n)2的几何意义是点A(a,b)与点B(m,n)两点间距离的平方;
∴(a-m)2+(b-n)2的几何意义是y=-x2+3lnx的图象上的点与y=x+2的图象上的点的距离的平方;
∵y=-x2+3lnx,
∴y′=-2x+3$\frac{1}{x}$=$\frac{3-2{x}^{2}}{x}$,(x>0)
故ymax=-$\frac{3}{2}$+$\frac{3}{2}$ln$\frac{3}{2}$<0,
故y=-x2+3lnx的图象始终在y=x+2的图象的下方,
令y′=-2x+3$\frac{1}{x}$=1得,
x=1;
此时y=-1+0=-1,
故切线方程为y=x-2;
y=x-1与y=x+2的距离为$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$;
故(a-m)2+(b-n)2的最小值为(2$\sqrt{2}$)2=8,
故选D.
点评 本题考查了导数的综合应用及转化的思想应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 10 | C. | 12 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{\sqrt{21}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
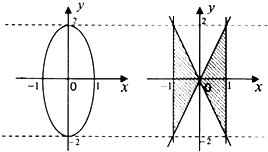 我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.
我国齐梁时代的数学家祖恒(公元前5-6世纪)提出了一条原理:“幂势既同,则买家不容异”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于平面的任何平面所截.如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等,设由椭圆x${\;}^{2}+\frac{{y}^{2}}{4}=1$所围成的平面图形绕y轴旋转一周得到的几何体(成为椭球体)体积为V1:由直线y=±2x,x=±1所围成的平面图形(如图阴影部分)绕y轴旋转一周所得到的几何体条件为V2:根据祖恒原理等知识,通过考察V2可得到V1的体积为$\frac{8}{3}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com