
分析 将直线方程代入双曲线方程,化为关于x的方程,利用方程的判别式,即可求得k的取值范围.
解答 解:由题意,直线y=kx-1代入双曲线x2-y2=4,可得x2-(kx-1)2=4,整理得(1-k2)x2+2kx-5=0.
(1)没有公共点,△=20-16k2<0,解得k>$\frac{\sqrt{5}}{2}$或k<-$\frac{\sqrt{5}}{2}$;
(2)有两个公共点,△=20-16k2>0,解得-$\frac{\sqrt{5}}{2}$<k<$\frac{\sqrt{5}}{2}$;
(3)只有一个公共点,当1-k2=0,k=±1时,符合条件;当1-k2≠0时,由△=20-16k2=0,解得k=±$\frac{\sqrt{5}}{2}$;
(4)交于异支两点,$\frac{-5}{1-{k}^{2}}$<0,解得-1<k<1;
(5)交于右支两点,△=20-16k2>0且$\frac{-5}{1-{k}^{2}}$>0,$\frac{-2k}{1-{k}^{2}}$>0,解得1<k<$\frac{\sqrt{5}}{2}$.
点评 本题考查直线与圆锥曲线的关系,解题的关键是将问题转化为方程根的问题,运用判别式解决,注意只有一个公共点时,不要忽视了与渐近线平行的情况,属于易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
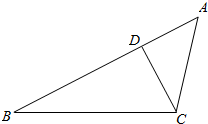 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com