
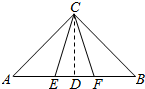
分析 取AB中点D,连接CD,设AB=6,则AC=BC=3$\sqrt{2}$,由余弦定理求出CE=CF=$\sqrt{10}$,再由余弦定理得cos∠ECF,由此能求出tan∠ECF.由半角公式求出cos∠DCF,sin∠DCF,再由cos∠BCF=cos(45°-∠DCF),能求出结果.
解答  解:取AB中点D,连接CD,
解:取AB中点D,连接CD,
设AB=6,则AC=BC=3$\sqrt{2}$,
由余弦定理可知cos45°=$\frac{A{C}^{2}+A{E}^{2}-C{E}^{2}}{2AC•AE}$=$\frac{18+4-C{E}^{2}}{2×3\sqrt{2}×2}$=$\frac{\sqrt{2}}{2}$,
解得CE=CF=$\sqrt{10}$,
再由余弦定理得cos∠ECF=$\frac{C{E}^{2}+C{F}^{2}-E{F}^{2}}{2CE•CF}$=$\frac{10+10-4}{2×\sqrt{10}×\sqrt{10}}$=$\frac{4}{5}$,
∴sin$∠ECF=\sqrt{1-(\frac{4}{5})^{2}}=\frac{3}{5}$,
∴tan∠ECF=$\frac{\frac{3}{5}}{\frac{4}{5}}$=$\frac{3}{4}$.
cos∠DCF=cos$\frac{1}{2}∠ECF$=$\sqrt{\frac{1+\frac{4}{5}}{2}}$=$\sqrt{\frac{9}{10}}$,sin∠DCF=sin$\frac{1}{2}∠ECF$=$\sqrt{\frac{1-\frac{4}{5}}{2}}$=$\sqrt{\frac{1}{10}}$,
cos∠BCF=cos(45°-∠DCF)=cos45°cos∠DCF+sin45°sin∠DCF=$\frac{\sqrt{2}}{2}$($\sqrt{\frac{9}{10}}+\sqrt{\frac{1}{10}}$)=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{3}{4}$,$\frac{2\sqrt{5}}{5}$.
点评 本题考查角的正切值、余弦值的求法,是中档题,解题时要认真审题,注意正弦定理、余弦定理、半角公式的合理运用.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 4 | 1 | 3 | 5 | 2 |
| A. | 1 | B. | 2 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
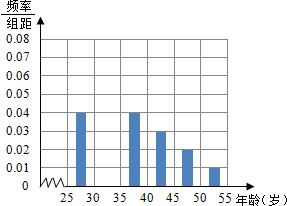 某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)
某班同学参加社会实践活动,本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如下(部分缺损)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com