
分析 讨论若焦点在x轴的正半轴上,设抛物线的方程为y2=2px,若焦点在y轴的正半轴上,可设x2=2ty(p,t>0),求出准线方程,由抛物线的定义,解方程即可得到所求方程.
解答 解:若焦点在x轴的正半轴上,设抛物线的方程为y2=2px,(p>0),
准线的方程为x=-$\frac{p}{2}$,
由抛物线的定义可得2=1+$\frac{p}{2}$,解得p=2,
可得抛物线的方程为y2=4x;
若焦点在y轴的正半轴上,可设x2=2ty(t>0),
准线的方程为y=-$\frac{t}{2}$,
由抛物线的定义可得,2=m+$\frac{t}{2}$,且1=2tm,
解得t=2$±\sqrt{3}$,
可得抛物线的方程为x2=2(2±$\sqrt{3}$)y.
故答案为:y2=4x或x2=2(2±$\sqrt{3}$)y.
点评 本题考查抛物线的方程的求法,注意运用待定系数法,考查解方程的运算求解能力,属于中档题.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:解答题
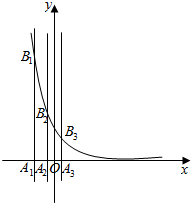 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
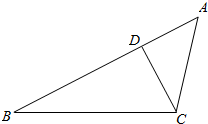 如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{5}$,D是边AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若d1-d2=0,则直线P1P2与直线l平行 | |
| B. | 若d1+d2=0,则直线P1P2与直线l平行 | |
| C. | 若d1+d2=0,则直线P1P2与直线l垂直 | |
| D. | 若d1•d2<0,则直线P1P2与直线l相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| B. | “am2<bm2”是”a<b”的必要不充分条件 | |
| C. | 命题p:存在x0∈R,使得x02+x0+1<0,则¬p:任意x∉R,都有x2+x+1≥0 | |
| D. | 命题“若x2<1,则-1<x<1”的逆否命题是若x≥1或x≤-1,则x2≥1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com