Question

4．已知函数f（x）=|log₄x|，正实数m、n满足m＜n，且f（m）=f（n），若f（x）在区间[m²，n]上的最大值为5，则m、n的值分别为2^-5、2⁵．

Answer 1

分析 由题意可知0＜m＜1＜n以及mn=1，又f（x）在区间[m²，n]上的最大值为5，可得出f（m²）=5，求出m，进而可得结论．

解答 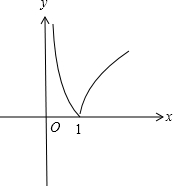解：函数f（x）=|log₄x|的图象如图，
∵正实数m、n满足m＜n，且f（m）=f（n），
∴0＜m＜1＜n，
又∵f（m）=f（n），∴|log₄m|=|log₄n|，
即-log₄m=log₄n，∴log₄mn=0，∴mn=1，
又∵函数在区间[m²，n]上的最大值为5、f（m²）=2f（m），
∴f（m²）=5，即|$lo{g}_{4}{m}^{2}$|=5，即$lo{g}_{4}{m}^{2}$=-5，即m²=4^-5，
∴m=2^-5，∴n=$\frac{1}{m}$=2⁵．
故答案为：2^-5、2⁵．

点评 本题考查对数函数的值域与最值，求解本题的关键是根据对数函数的性质判断出0＜m＜1＜n、mn=1及f（x）在区间[m²，n]上的最大值的位置．根据题设条件灵活判断对解题很重要．注意解题方法的积累，属于中档题．