
分析 分别以$\overrightarrow{a},\overrightarrow{b}$所在的直线为x,y轴建立直角坐标系,分类讨论:当{|$\overrightarrow a$|,|$\overrightarrow b$|}={1,2},|$\overrightarrow{c}$|=3,设$\overrightarrow{c}=(x,y)$,则x2+y2=9,则$\overrightarrow a$+$\overrightarrow b$+$\overrightarrow c$=(1+x,2+y),有|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|=$\sqrt{(x+1)^{2}+(y+2)^{2}}$的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(-1,-2)的距离的最大值;其他情况同理,然后求出各种情况的最大值进行比较即可.
解答 解:分别以$\overrightarrow{a},\overrightarrow{b}$所在的直线为x,y轴建立直角坐标系,
①当{|$\overrightarrow a$|,|$\overrightarrow b$|}={1,2},|$\overrightarrow{c}$|=3,则$\overrightarrow{a}+\overrightarrow{b}=(1,2)$,
设$\overrightarrow{c}=(x,y)$,则x2+y2=9,
∴$\overrightarrow a$+$\overrightarrow b$+$\overrightarrow c$=(1+x,2+y),
∴|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|=$\sqrt{(x+1)^{2}+(y+2)^{2}}$的最大值,其几何意义是圆x2+y2=9上点(x,y)与定点(-1,-2)的距离的最大值为$3+\sqrt{(0+2)^{2}+(0+1)^{2}}$=3+$\sqrt{5}$;
②且{|$\overrightarrow a$|,|$\overrightarrow b$|}={1,3},|$\overrightarrow{c}$|=2,则$\overrightarrow{a}+\overrightarrow{b}=(1,3)$,x2+y2=4,
∴$\overrightarrow a$+$\overrightarrow b$+$\overrightarrow c$=(1+x,3+y)
∴|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|=$\sqrt{(x+1)^{2}+(y+3)^{2}}$的最大值,其几何意义是圆x2+y2=4上点(x,y)与定点(-1,-3)的距离的最大值为2+$\sqrt{(0+1)^{2}+(0+3)^{2}}$=2+$\sqrt{10}$,
③{|$\overrightarrow a$|,|$\overrightarrow b$|}={2,3},|$\overrightarrow{c}$|=1,则$\overrightarrow{a}+\overrightarrow{b}=(2,3)$,
设$\overrightarrow{c}=(x,y)$,则x2+y2=1
∴$\overrightarrow a$+$\overrightarrow b$+$\overrightarrow c$=(2+x,3+y)
∴|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|=$\sqrt{(x+2)^{2}+(y+3)^{2}}$的最大值,其几何意义是在圆x2+y2=1
上取点(x,y)与定点(-2,-3)的距离的最大值为1+$\sqrt{(0+2)^{2}+(0+3)^{2}}$=1+$\sqrt{13}$
∵$1+\sqrt{13}<3+\sqrt{5},2+\sqrt{10}<3+\sqrt{5}$,
故|$\overrightarrow a$+$\overrightarrow b$+$\overrightarrow c$|的最大值为3+$\sqrt{5}$.
故答案为:3+$\sqrt{5}$
点评 本题主要考查了向量的模的求解,解题的关键是圆的性质的应用:在圆外取一点,使得其到圆上点的距离的最大值:r+d(r为该圆的半径,d为该点与圆心的距离).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
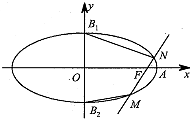 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com