
∑÷Œˆ £®¢Ò£©¿˚”√an+1=Sn+n£¨µ√µΩan+1-an=Sn-Sn-1+1=an+1£¨Õ∆≥ˆ{an+1}µƒ ˝¡–Ãÿ’˜£¨»ª∫Û«ÛΩ‚{an}µƒÕ®œÓπ´ Ω£Æ£Æ
£®¢Ú£©£®¢°£©¿˚”√ ˝¡–µƒ∫Õ£¨Ω·∫œµ»≤Ó ˝¡–º¥ø…«Û≥ˆ{bn}µƒÕ®œÓπ´ Ωbn=b1+£®n-1£©d=n+1£Æ
£®¢¢£©Õ®π˝ ˝¡–µƒÕ®œÓπ´ Ω£¨¿˚”√∑≈Àı∑®“‘º∞¡–œÓ«Û∫Õ£¨Õ∆≥ˆΩ·π˚º¥£Æ
Ω‚¥ £®±æÂ13∑÷£©
£®¢Ò£©Ω‚£∫”…an+1=Sn+n£¨µ√an=Sn-1+£®n-1£©£®n£æ1£©£¨°≠£®1 ∑÷£©
¡Ω Ωœýºı£¨µ√an+1-an=Sn-Sn-1+1=an+1£¨
°ýan+1=2an+1£¨º¥an+1+1=2£®an+1£©£®n£æ1£©£Æ°≠£®2 ∑÷£©
°þa1=2£¨
°ýa2=S1+1=a1+1=3£Æ°≠£®3 ∑÷£©
°ý${a_n}+1={2^{n-2}}£®{a_2}+1£©={2^n}$£®n£æ1£©£Æ°≠£®4 ∑÷£©
°ý{an}µƒÕ®œÓπ´ ΩŒ™${a_n}=\left\{{\begin{array}{l}{2£¨n={1_{\;}}}\\{{2^n}-1{£¨_{\;}}n£æ1}\end{array}}\right.$°≠£®5 ∑÷£©
£®¢Ú£©Ω‚£∫£®¢°£©°þ{bn}Œ™µ»≤Ó ˝¡–£¨«“T3=9£¨
°ýb2=3£Æ°≠£®6 ∑÷£©
…Ë{bn}µƒπ´≤ÓŒ™d£¨‘Úb1=3-d£¨b3=3+d£Æ
°þa1=2£¨a2=3£¨a3=7£¨
°ýa1+b1=5-d£¨a2+b2=6£¨${a_3}+\frac{1}{2}{b_3}=\frac{17}{2}+\frac{1}{2}d$£Æ°≠£®7 ∑÷£©
°þa1+b1£¨a2+b2£¨${a_3}+\frac{1}{2}{b_3}$≥…µ»±» ˝¡–£¨
°ý£®5-d£©£®17+d£©=72£Æ
°ýd=1ªÚd=-13£®≤ª∫œÃ‚“‚£¨…·»•£©£Æ°≠£®8 ∑÷£©
°ýbn=b1+£®n-1£©d=n+1£Æ°≠£®9 ∑÷£©
£®¢¢£©°þ$\frac{1}{b_k^2}=\frac{1}{{{{£®k+1£©}^2}}}£º\frac{1}{{{{£®k+1£©}^2}-1}}=\frac{1}{k£®k+2£©}=\frac{1}{2}£®\frac{1}{k}-\frac{1}{k+2}£©$£®k° N*£©£¨£®10∑÷£©
°ý$\sum_{i=1}^n{\frac{1}{b_i^2}£º\frac{1}{2}}£®1-\frac{1}{3}£©+\frac{1}{2}£®\frac{1}{2}-\frac{1}{4}£©+°≠+\frac{1}{2}£®\frac{1}{n}-\frac{1}{n+2}£©$°≠£®11∑÷£©
=$\frac{1}{2}£®1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2}£©$$£º\frac{1}{2}£®1+\frac{1}{2}£©=\frac{3}{4}$£Æ°≠£®13∑÷£©
µ„∆¿ ±æÂøº≤È ˝¡–µƒ◊€∫œ”¶”√£¨ ˝¡–«Û∫Õ£¨∑≈Àı∑®µƒ”¶”√£¨øº≤È∑÷ŒˆŒ Ã‚Ω‚æˆŒ µƒƒÐ¡¶£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | c£æa£æb | B£Æ | b£æc£æa | C£Æ | c£æb£æa | D£Æ | b£æa£æc |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
| º◊ | ““ | ±˚ | |
| A | 100 | 150 | m |
| B | 300 | 450 | 600 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | ¢Ÿ¢€⇒¢⁄¢ÐªÚ¢⁄¢€⇒¢Ÿ¢Ð | B£Æ | ¢Ÿ¢€⇒¢⁄¢Ð | C£Æ | ¢⁄¢€⇒¢Ÿ¢Ð | D£Æ | ¢Ÿ¢Ð⇒¢⁄¢€ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫Ω‚¥Ã‚
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 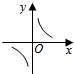 | B£Æ | 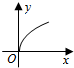 | C£Æ | 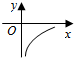 | D£Æ | 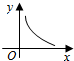 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫ÃÓø’Â
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com