
���� ������Բ�IJ������̱��Σ�Ȼ��ƽ�����������ͨ���̣�չ�����Ǻ͵����ң�����x=��cos�ȣ�y=��sin�����ֱ�ߵ�ֱ�����귽�̣�
������P��$\sqrt{3}$cos�գ�sin�գ����ɵ㵽ֱ�ߵľ��빫ʽ�õ����룬�������Ǻ�������ֵ��ô𰸣�
��� �⣺������$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$����$\left\{\begin{array}{l}{\frac{x}{\sqrt{3}}=cos��}\\{y=sin��}\end{array}\right.$����ʽƽ�����͵�$\frac{{x}^{2}}{3}+{y}^{2}=1$��
������C1����ͨ����Ϊ$\frac{{x}^{2}}{3}+{y}^{2}=1$��
�ɦ�cos����+$\frac{��}{3}$��=2����$��cos��cos\frac{��}{3}-��sin��sin\frac{��}{3}=2$��
��$\frac{1}{2}��cos��-\frac{\sqrt{3}}{2}��sin��=2$����$x-\sqrt{3}y-4=0$��
������C2��ֱ�����귽��Ϊ$x-\sqrt{3}y-4=0$��
������P��$\sqrt{3}$cos�գ�sin�գ���������֪����P��ֱ��C2����Ϊ
$d=\frac{|\sqrt{3}cos��-\sqrt{3}sin��-4|}{2}$=$\frac{|\sqrt{6}cos��\frac{��}{4}+�գ�-4|}{2}��\frac{4-\sqrt{6}}{2}$��
����=-$\frac{��}{4}$ʱ��dȡ��Сֵ$\frac{4-\sqrt{6}}{2}$��
��ʱ��P��$\frac{\sqrt{6}}{2}$��$-\frac{\sqrt{2}}{2}$����
���� ���⿼��������̻���ͨ���̣����鼫���귽�̻�ֱ�����귽�̣�ѵ���˵㵽ֱ�ߵľ��빫ʽ��Ӧ�ã����������Ǻ�����ֵ�����ǻ����⣮


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
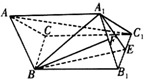 ��ͼ��б������ABC-A1B1C1�У�A1B1=A1C1����E��F�ֱ���B1C1��A1B1���е㣬AA1=AB=BE=1����A1AB=60�㣮
��ͼ��б������ABC-A1B1C1�У�A1B1=A1C1����E��F�ֱ���B1C1��A1B1���е㣬AA1=AB=BE=1����A1AB=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6+3$\sqrt{2}$ | B�� | 5+2$\sqrt{3}$ | C�� | 8 | D�� | 6+2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
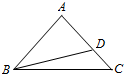 ��ͼ���ڡ�ABC�У�AB=AC��D���߶�AC�ϣ���AC=$\sqrt{2}$AD��BD=1��
��ͼ���ڡ�ABC�У�AB=AC��D���߶�AC�ϣ���AC=$\sqrt{2}$AD��BD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com