
分析 ①设z=a+bi,a,b∈R,利用两个复数相等的充要条件,得到关于a,b的方程组,解得即可,
②先验证n=1成立,再假设n=k成立,推导n=k+1成立即可.
解答 解:①设z=a+bi,a,b∈R,
∵|z|-z=$\frac{10}{1-2i}$=$\frac{10(1+2i)}{(1-2i)(1+2i)}$=2+4i,
∴$\sqrt{{a}^{2}+{b}^{2}}$-a-bi=2+4i,
即$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}-a=2}\\{-b=4}\end{array}\right.$,
解得a=3,b=4,
故z=3+4i,
②:(1)当n=1时,13+5=6,显然能被6整除,
(2)假设n=k时,k3+5k,(k∈N*)能被6整除
则当n=k+1时,(k+1)3+5(k+1)=(k3+5k)+3k(k+1)+6,
由于假设k3+5k能够被6整除,而k(k+1)能够被2整除,因此3k(k+1)+6能够被6整除,
故当n=k+1时,能被6整除,
由(1),(2)可知n3+5n(n∈N*)能被6整除
点评 本题考查复数的模的定义,两个复数相等的充要条件,考查了数学归纳法、乘法公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0)∪(9,+∞) | C. | (9,+∞) | D. | (-∞,1)∪(9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
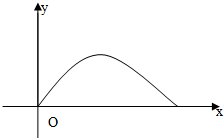 如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.
如图,在平面直角坐标系xOy中,x轴在地平面上,y轴垂直于地面,x轴、y轴上的单位长度都为1km,某炮位于坐标原点处,炮弹发射后,其路径为抛物线y=kx-$\frac{1}{20}(1+{k^2}){x^2}$的一部分,其中k与炮弹的发射角有关且k>0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com