Question

15．（1）已知直线l的纵截距为-1，倾斜角是直线l₁：3x+4y-1=0的倾斜角的一半，求直线l的方程．
（2）已知直线l过点A（-2，4），分别交x轴、y轴于点B、C且满足$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{AC}$，求直线l的方程．

Answer 1

分析 （1）设出已知直线的倾斜角2α，得到tan2α的值，进一步求出tanα的值，由直线方程的斜截式得答案；
（2）设出B、C的坐标，得到$\overrightarrow{BA}、\overrightarrow{AC}$的坐标，由$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{AC}$求得直线l的横截距和纵截距，由截距式方程得答案．

解答 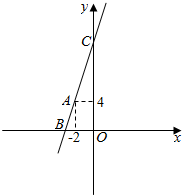解：（1）设直线3x+4y-5=0的倾斜角为2α，
则所求直线的倾斜角为α，
由题意知tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=-$\frac{3}{4}$，
∵0≤2α＜π，∴0≤α＜$\frac{π}{2}$，
∴k=tanα=3或k=tanα=-$\frac{1}{3}$（舍去）．
∴所求直线方程为：y=3x-1，
即3x-y-1=0；
（2）如图，由$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{AC}$，可知直线l交x轴于负半轴，交y轴于坐标轴．
设B（a，0），C（0，b），又A（-2，4），
则$\overrightarrow{BA}=（-2-a，4），\overrightarrow{AC}=（2，b-4）$，
由$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{AC}$，得$（-2-a，4）=（1，\frac{b-4}{2}）$，
∴$\left\{\begin{array}{l}{-2-a=1}\\{4=\frac{b-4}{2}}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=-3}\\{b=12}\end{array}\right.$．
∴直线l的方程为$\frac{x}{-3}+\frac{y}{12}=1$，即4x-y+12=0．

点评 本题考查直线的倾斜角，考查了倾斜角与斜率的关系，考查平面向量的坐标运算，训练了直线方程的求法，是基础题．