
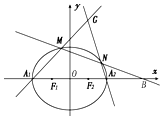
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.分析 (Ⅰ)设点A1(-a,0),F2(c,0),由题意得a=4-2c,由椭圆的离心率$e=\frac{c}{a}=\frac{1}{2}$,得a=2c,求出a,b,由此能示出椭圆C的方程.
(Ⅱ)法一:根据椭圆的对称性猜测点G是与y轴平行的直线x=x0上.假设当点M为椭圆的上顶点时,直线l的方程为$\sqrt{3}x+4y-4\sqrt{3}=0$,此时点N$(\frac{8}{5},\frac{{3\sqrt{3}}}{5})$,联立直线${l_{{A_1}M}}:\sqrt{3}x-2y+2\sqrt{3}=0$和直线${l_{{A_2}N}}:3\sqrt{3}x+2y-6\sqrt{3}=0$可得点$G(1,\frac{{3\sqrt{3}}}{2})$,猜想点G在直线x=1上,对猜想给予证明,得到点G在定直线上x=1上.
法二:设M(x1,y1),N(x2,y2),G(x3,y3),由B,M,N三点共线,得:2x1x2-5(x1+x2)+8=0,再由A1,M,G三点共线,A2,N,G三点共线,推导出点G在定直线x=1上.
法三:设l的方程为y=k(x-4),M(x1,y1),N(x2,y2).由$\left\{{\begin{array}{l}{y=k(x-4)}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$得(3+4k2)x2-32k2x+64k2-12=0,由此利用根的判别式、韦达定理,结合A1,M,G三点共线,A2,N,G三点共线,推导出点G在定直线x=1上.
解答 解:(Ⅰ)设点A1(-a,0),F2(c,0),由题意可知:$c=\frac{-a+4}{2}$,即a=4-2c①
又因为椭圆的离心率$e=\frac{c}{a}=\frac{1}{2}$,即a=2c②
联立方程①②可得:a=2,c=1,则b2=a2-c2=3
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.-------(5分)
解:(Ⅱ)解法一:根据椭圆的对称性猜测点G是与y轴平行的直线x=x0上.
假设当点M为椭圆的上顶点时,直线l的方程为$\sqrt{3}x+4y-4\sqrt{3}=0$,此时点N$(\frac{8}{5},\frac{{3\sqrt{3}}}{5})$,
则联立直线${l_{{A_1}M}}:\sqrt{3}x-2y+2\sqrt{3}=0$和直线${l_{{A_2}N}}:3\sqrt{3}x+2y-6\sqrt{3}=0$可得点$G(1,\frac{{3\sqrt{3}}}{2})$
据此猜想点G在直线x=1上,下面对猜想给予证明:-------(7分)
设M(x1,y1),N(x2,y2),联立方程$\left\{\begin{array}{l}y=k(x-4)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$可得:(3+4k2)x2-32k2x+64k2-12=0,△>0
由韦达定理可得${x_1}+{x_2}=\frac{{32{k^2}}}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{64{k^2}-12}}{{3+4{k^2}}}$(*)-------(9分)
因为直线${l_{{A_1}M}}:y=\frac{y_1}{{{x_1}+2}}(x+2)$,${l_{{A_2}N}}:y=\frac{y_2}{{{x_2}-2}}(x-2)$,
联立两直线方程得$\frac{y_1}{{{x_1}+2}}(x+2)=\frac{y_2}{{{x_2}-2}}(x-2)$(其中x为G点的横坐标)即证:$\frac{{3{y_1}}}{{{x_1}+2}}=\frac{{-{y_2}}}{{{x_2}-2}}$,
即3k(x1-4)•(x2-2)=-k(x2-4)•(x1+2),即证4x1x2-10(x1+x2)+16=0-------(11分)
将(*)代入上式可得$\frac{{4•(64{k^2}-12)}}{{3+4{k^2}}}-\frac{{10×32{k^2}}}{{3+4{k^2}}}+16=0?16{k^2}-3-20{k^2}+3+4{k^2}=0$
此式明显成立,原命题得证.所以点G在定直线上x=1上.-------(12分)
解法二:设M(x1,y1),N(x2,y2),G(x3,y3),x1,x2,x3两两不等,
因为B,M,N三点共线,所以$\frac{y_1}{{{x_1}-4}}=\frac{y_2}{{{x_2}-4}}⇒\frac{{{y_1}^2}}{{{{({x_1}-4)}^2}}}=\frac{{{y_2}^2}}{{{{({x_2}-4)}^2}}}⇒\frac{{3(1-\frac{x_1^2}{4})}}{{{{({x_1}-4)}^2}}}=\frac{{3(1-\frac{x_2^2}{4})}}{{{{({x_2}-4)}^2}}}$,
整理得:2x1x2-5(x1+x2)+8=0-------(8分)
又A1,M,G三点共线,有:$\frac{y_3}{{{x_3}+2}}=\frac{y_1}{{{x_1}+2}}$①
又A2,N,G三点共线,有:$\frac{y_3}{{{x_3}-2}}=\frac{y_2}{{{x_2}-2}}$②,
将①与②两式相除得:$\frac{{{x_3}+2}}{{{x_3}-2}}=\frac{{{y_2}({x_1}+2)}}{{{y_1}({x_2}-2)}}⇒{(\frac{{{x_3}+2}}{{{x_3}-2}})^2}=\frac{{{y_2}^2{{({x_1}+2)}^2}}}{{{y_1}^2{{({x_2}-2)}^2}}}=\frac{{3(1-\frac{x_2^2}{4}){{({x_1}+2)}^2}}}{{3(1-\frac{x_1^2}{4}){{({x_2}-2)}^2}}}=\frac{{({x_2}+2)({x_1}+2)}}{{({x_1}-2)({x_2}-2)}}$
即${(\frac{{{x_3}+2}}{{{x_3}-2}})^2}=\frac{{({x_2}+2)({x_1}+2)}}{{({x_1}-2)({x_2}-2)}}=\frac{{{x_1}{x_2}+2({x_1}+{x_2})+4}}{{{x_1}{x_2}-2({x_1}+{x_2})+4}}$,-------(10分)
将2x1x2-5(x1+x2)+8=0即${x_1}{x_2}=\frac{5}{2}({x_1}+{x_2})-4=0$代入得:${(\frac{{{x_3}+2}}{{{x_3}-2}})^2}=9$
解得x3=4(舍去)或x3=1,所以点G在定直线x=1上.-------(12分)
解法三:由题意知l与x轴不垂直,设l的方程为y=k(x-4),M(x1,y1),N(x2,y2).
由$\left\{{\begin{array}{l}{y=k(x-4)}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$得(3+4k2)x2-32k2x+64k2-12=0,△>0.-------(7分)
设M(x1,y1),N(x2,y2),G(x3,y3),x1,x2,x3两两不等,
则${x_1}+{x_2}=\frac{{32{k^2}}}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{64{k^2}-12}}{{3+4{k^2}}}$,$|{x_1}-{x_2}|=\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\frac{{12\sqrt{1-4{k^2}}}}{{3+4{k^2}}}$,
由A1,M,G三点共线,有:$\frac{y_3}{{{x_3}+2}}=\frac{y_1}{{{x_1}+2}}$①
由A2,N,G三点共线,有:$\frac{y_3}{{{x_3}-2}}=\frac{y_2}{{{x_2}-2}}$②
①与②两式相除得:$\frac{{{x_3}+2}}{{{x_3}-2}}=\frac{{{y_2}({x_1}+2)}}{{{y_1}({x_2}-2)}}=\frac{{k({x_2}-4)({x_1}+2)}}{{k({x_1}-4)({x_2}-2)}}=\frac{{{x_1}{x_2}-({x_1}+{x_2})+3({x_1}-{x_2})-8}}{{{x_1}{x_2}-3({x_1}+{x_2})+({x_1}-{x_2})+8}}=-\frac{1}{3}$-------(10分)
解得x3=4(舍去)或x3=1,所以点G在定直线x=1上.-------(12分)
点评 本题考查椭圆方程的求法,考查点是否在定直线上的判断与证明,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理、三点共线等知识点的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | [-3,-2] | C. | (-∞,-3)∪(-2,+∞) | D. | (-∞,-3)∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
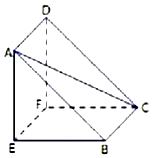 如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.
如图所示为一名曰“堑堵”的几何体,已知AE⊥底面BCFE,DF∥AE,DF=AE=1,CE=$\sqrt{7}$,四边形ABCD是正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
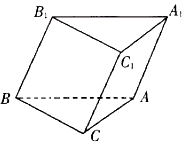 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com