
分析 (1)利用数列的递推关系式推出${a_{n+1}}-\frac{1}{2}=3({a_n}-\frac{1}{2})(n∈{N^*})$,然后证明{bn}是以1为首项,3为公比的等比数列.
(2)求出${b_n}={3^{n-1}}$,化简${a_n}={3^{n-1}}+\frac{1}{2}$,推出${c_n}={log_3}({3^{n-1}}+\frac{1}{2})>{log_3}{3^{n-1}}=n-1$,然后通过数列求和,证明结果.
解答 (本小题满分12分)
解:(1)由题可知${a_{n+1}}-\frac{1}{2}=3({a_n}-\frac{1}{2})(n∈{N^*})$,
从而有bn+1=3bn,${b_1}={a_1}-\frac{1}{2}=1$,
所以{bn}是以1为首项,3为公比的等比数列.(6分)
(2)由(1)知${b_n}={3^{n-1}}$,
从而${a_n}={3^{n-1}}+\frac{1}{2}$,${c_n}={log_3}({3^{n-1}}+\frac{1}{2})>{log_3}{3^{n-1}}=n-1$,
有${T_n}={c_1}+{c_2}+…+{c_n}>0+1+2+…n-1=\frac{n(n-1)}{2}$,
所以${T_n}>\frac{n(n-1)}{2}$.(12分)
点评 本题考查等比数列及利用不等式性质证明与数列前n项和有关的不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
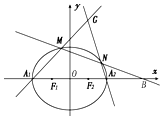 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
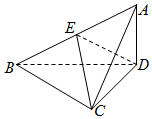 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.
如图长方体ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别为CB1、CD1、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
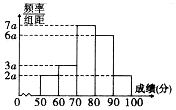 在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.
在某市举办的安全教育知识竞赛中,抽取1800名学生的成绩(单位:分),其频率分布直方图如图所示,则成绩落在[50,60)中的学生人数为180.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com