
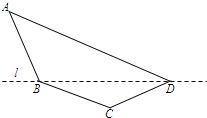
 某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一上展览沙盘,现谷在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示,为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.| 3 |
| 1 |
| 2 |
| (x2-4)(x2-14x+49) |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2A |
| (x2-4)(x2-14x+49) |
| 1 |
| 2 |
| 3 |
| 3 |


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| A、p∧q为真命题 |
| B、(¬p)∧q为真命题 |
| C、p∨q为假命题 |
| D、p∨(¬q)为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com