
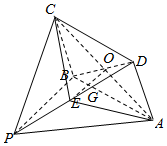
 ��ͼ��ʾ�ļ�����P-ABCD�У��ı���ABCDΪ���Σ���ABC=120�㣬AB=a��$PB=\sqrt{3}a$��PB��AB��ƽ��ABCD��ƽ��PAB��AC��BD=O��EΪPD���е㣬GΪƽ��PAB����һ�㣮
��ͼ��ʾ�ļ�����P-ABCD�У��ı���ABCDΪ���Σ���ABC=120�㣬AB=a��$PB=\sqrt{3}a$��PB��AB��ƽ��ABCD��ƽ��PAB��AC��BD=O��EΪPD���е㣬GΪƽ��PAB����һ�㣮���� ��1�������֪OΪBD���е㣬��EΪPD���е㣬�ɵ�OE��PB������G��ֱ��PB�ϣ���ֱ��PB��Ϊ������ֱ��l����OE��l������G����ֱ��PB�ϣ���ƽ��PAB�ڣ�����G��ֱ��l��ʹl��PB����ƽ�й����ɵ�OE��l������G�����ֱ��lʹOE��l��
��2������EA��EC����ƽ��ACE��������ֳ������֣����õȻ������VD-AEC=VE-ACD=$\frac{1}{3}{S_{��ACD}}•EO$=$\frac{1}{4}{V_{P-ABCD}}=\frac{1}{8}{a^3}$������VP-ABCD-VD-EAC��ú���AECBP�������
���  �⣺��1����G�����ֱ��lʹOE��l���������£�
�⣺��1����G�����ֱ��lʹOE��l���������£�
�����֪OΪBD���е㣬��EΪPD���е㣬
���ڡ�PBD�У���OE��PB��
����G��ֱ��PB�ϣ���ֱ��PB��Ϊ������ֱ��l��
��OE��l��
����G����ֱ��PB�ϣ���ƽ��PAB�ڣ�
����G��ֱ��l��ʹl��PB��
��OE��PB����OE��l��
����G�����ֱ��lʹOE��l��
��2������EA��EC����ƽ��ACE��������ֳ������֣�
����D-AEC�뼸����AECBP����ͼ��ʾ����
��ƽ��ABCD��ƽ��PAB���ҽ���ΪAB��
��PB��AB����PB��ƽ��ABCD��
��PBΪ������P-ABCD�ĸߣ�
���ı���ABCDΪ���Σ���ABC=120�㣬AB=a��$PB=\sqrt{3}a$��
��S�ı���ABCD=2��$\frac{{\sqrt{3}}}{4}{a^2}=\frac{{\sqrt{3}}}{2}{a^2}$��
��${V_{P-ABCD}}=\frac{1}{3}{S_{�ı���ABCD}}•PB$=$\frac{1}{3}��\frac{{\sqrt{3}}}{2}{a^2}��\sqrt{3}a=\frac{1}{2}{a^3}$��
��OE��PB��OE=$\frac{1}{2}PB$����OE��ƽ��ACD��
��VD-AEC=VE-ACD=$\frac{1}{3}{S_{��ACD}}•EO$=$\frac{1}{4}{V_{P-ABCD}}=\frac{1}{8}{a^3}$��
�༸����AECBP�����V=VP-ABCD-VD-EAC=$\frac{1}{2}{a^3}-\frac{1}{8}{a^3}=\frac{3}{8}{a^3}$��
���� ���⿼��ƽ����ƽ�洹ֱ�����ʣ�����ռ�����������˼ά������ѵ�������õȻ�������������������е��⣮


 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3+2$\sqrt{2}$ | B�� | 3+2$\sqrt{3}$ | C�� | 7 | D�� | 11 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������E-ABCD�У�����ABCDΪ�����Σ�AE��ƽ��CDE����֪AE=DE=2��FΪ�߶�DF���е㣮
��ͼ��������E-ABCD�У�����ABCDΪ�����Σ�AE��ƽ��CDE����֪AE=DE=2��FΪ�߶�DF���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����������S-ABCD�У�AB��AD��AB��CD��CD=3AB=3��
��ͼ����������S-ABCD�У�AB��AD��AB��CD��CD=3AB=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������������У�б��l�Ϸ�����1��ʼ��ͷ��ʾ�������һ��������У�1��3��3��4��6��5��10����������ǰn���ΪSn����S19����283��
��ͼ������������У�б��l�Ϸ�����1��ʼ��ͷ��ʾ�������һ��������У�1��3��3��4��6��5��10����������ǰn���ΪSn����S19����283���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com