
 如图,在四棱锥中S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,
如图,在四棱锥中S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,分析 (1)证明SE⊥AD,SE⊥BE.推出BE⊥CE.证明BE⊥平面SEC,然后证明平面SBE⊥平面SEC.
(2)以EB为x轴,以EC为y轴,以ES为z轴,建立空间直角坐标系.求出相关点的坐标,求出平面SBC的法向量,设直线CE与平面SBC所成角为θ,通过向量的数量积求解直线CE与平面SBC所成角的正弦值即可.
解答 解:(1)证明:∵平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,SE?平面SAD,SE⊥AD,
∴SE⊥平面ABCD,…(2分)
∵BE?平面ABCD,∴SE⊥BE.∵CD=3AB=3,AE=ED=$\sqrt{3}$,∴∠AEB=30°,∠CED=60°.
所以∠BEC=90°即BE⊥CE.…(4分)
结合SE∩CE=E得BE⊥平面SEC,∵BE?平面SBE,∴平面SBE⊥平面SEC.…(6分)
(2)由(1)知,直线ES,EB,EC两两垂直.
如图,以EB为x轴,以EC为y轴,以ES为z轴,建立空间直角坐标系.
则$E(0,0,0),C(0,2\sqrt{3},0),S(0,0,1),B(2,0,0)$,
∴$\overrightarrow{CB}=(2,-2\sqrt{3},0),\overrightarrow{CS}=(0,-2\sqrt{3},1)$.
设平面SBC的法向量为$\overrightarrow n=(x,y,z)$,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{CB}=0\\ \overrightarrow n•\overrightarrow{CS}=0\end{array}\right.$
解得一个法向量$\overrightarrow n=(\sqrt{3},1,2\sqrt{3})$,…(9分)
设直线CE与平面SBC所成角为θ,
又$\overrightarrow{CE}=(0,-2\sqrt{3},0)$,
则$sinθ=|{\frac{{\overrightarrow n•\overrightarrow{CE}}}{{|{\overrightarrow n}|•|{\overrightarrow{CE}}|}}}|=\frac{1}{4}$.
所以直线CE与平面SBC所成角的正弦值$\frac{1}{4}$.…(12分)
点评 本题考查直线与平面所成角的求法,直线与平面垂直的判定定理的应用,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
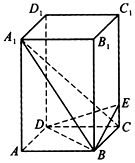 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.
如图所示的几何体P-ABCD中,四边形ABCD为菱形,∠ABC=120°,AB=a,$PB=\sqrt{3}a$,PB⊥AB,平面ABCD⊥平面PAB,AC∩BD=O,E为PD的中点,G为平面PAB内任一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},\sqrt{e}})$ | B. | $[{\frac{1}{2},\sqrt{e}})$ | C. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}}]$ | D. | $({\frac{1}{2},\frac{{\sqrt{e}}}{e}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 9 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com