
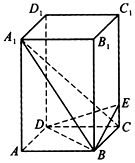
 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1分析 以D点为原点,以$\overrightarrow{DA,}$$\overrightarrow{DC}$,$\overrightarrow{D{D}_{1}}$的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系 易知D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、A1(2,0,4)、B1(2,2,4)、C1(0,2,4)、D1(0,0,4)、E(0,2,1),
(1)由$\overrightarrow{{A}_{1}C}•\overrightarrow{BE}=4+0-4=0$,$\overrightarrow{{A}_{1}C}•\overrightarrow{DB}=-4+4+0=0$,即A1C⊥DB,且A1C⊥BE.又BE∩DB=B,得A1C⊥平面BED;
(2)知$\overrightarrow{{A}_{1}C}=(-2,2,-4)$是平面BDE的一个法向量 由cos$<\overrightarrow{{A}_{1}C},\overrightarrow{{A}_{1}B}>$=$\frac{20}{\sqrt{24}×\sqrt{20}}=\frac{\sqrt{30}}{6}$,可得AA1B与平面BDE所成角的正弦值.
解答 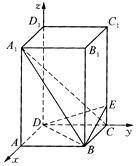 解:(1)以D点为原点,以$\overrightarrow{DA,}$$\overrightarrow{DC}$,$\overrightarrow{D{D}_{1}}$的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系(如图),
解:(1)以D点为原点,以$\overrightarrow{DA,}$$\overrightarrow{DC}$,$\overrightarrow{D{D}_{1}}$的方向为x轴、y轴、z轴的正方向,建立空间直角坐标系(如图),
易知D(0,0,0)、A(2,0,0)、B(2,2,0)、C(0,2,0)、A1(2,0,4)、B1(2,2,4)、
C1(0,2,4)、D1(0,0,4)、E(0,2,1)…(2分)
从而$\overrightarrow{{A}_{1}C}=(-2,2,-4)$,$\overrightarrow{DB}=(2,2,0)$,$\overrightarrow{BE}=(-2,0,0)$,
则$\overrightarrow{{A}_{1}C}•\overrightarrow{BE}=4+0-4=0$,$\overrightarrow{{A}_{1}C}•\overrightarrow{DB}=-4+4+0=0$
即A1C⊥DB,且A1C⊥BE.又BE∩DB=B,故A1C⊥平面BED;.…(6分)
(2)由(1)知$\overrightarrow{{A}_{1}C}=(-2,2,-4)$是平面BDE的一个法向量,…(8分)
而$\overrightarrow{{A}_{1}B}=(0,2,-4)$,因此cos$<\overrightarrow{{A}_{1}C},\overrightarrow{{A}_{1}B}>$=$\frac{20}{\sqrt{24}×\sqrt{20}}=\frac{\sqrt{30}}{6}$,…(10分)
从而AA1B与平面BDE所成角的正弦值为$\frac{\sqrt{30}}{6}$.…(12分)
点评 本题考查了空间线面垂直的判定,线面角的求解,属于中档题,


科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,
如图,已知四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+2$\sqrt{2}$ | B. | 3+2$\sqrt{3}$ | C. | 7 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4) | B. | (-1,-1) | C. | (1,1)或(-1,-1) | D. | (1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥中S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,
如图,在四棱锥中S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com