
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)根据直线和双曲线的位置关系进行判断.
(2)根据四点共面的等价条件进行判断.
(3)根据四点共面的等价条件进行判断.
(4)根据极坐标成立的条件进行判断.
解答 解:(1)由双曲线方程得a=2,c=3,即直线l:y=k(x-3)过双曲线的右焦点,
∵双曲线的两个顶点之间的距离是2a=4,a+c=2+3=5,
∴当直线与双曲线左右两支各有一个交点时,当k=0时2a=4,
则满足|AB|=5的直线有2条,
当直线与实轴垂直时,
当x=c=3时,得$\frac{9}{4}$-$\frac{y^2}{5}$=1,即$\frac{y^2}{5}$=$\frac{5}{4}$,即y2=$\frac{25}{4}$,则y=±$\frac{5}{2}$,
此时通径长为5,若|AB|=5,则此时直线AB的斜率不存在,故不满足条件.综上可知有2条直线满足|AB|=5,故(1)错误,
(2)∵$\frac{1}{6}$+$\frac{1}{3}$+$\frac{1}{2}$=1,∴P,A,B,C四点共面,故(2)正确,
(3)∵2-1+2=-1≠1,∴P,A,B,C四点一定不共面,故(3)正确,
(4)当θ=$\frac{π}{3}$时,1-2cosθ=1-2cos$\frac{π}{3}$=1-2×$\frac{1}{2}$=1-1=0,
此时曲线ρ=$\frac{1}{1-2cosθ}$无意义,即直线θ=$\frac{π}{3}$(ρ∈R)与曲线ρ=$\frac{1}{1-2cosθ}$(ρ∈R)没有公共点,故(4)正确,
故选:C
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤1} | B. | {x|-1≤x<0} | C. | {x|0≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{4},2}]$ | B. | $[{-\frac{1}{4},2})$ | C. | $[{-2,\frac{1}{4}})$ | D. | $({-2,\frac{1}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
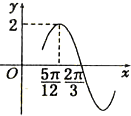 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{1}{12}$π] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x=y,则$\frac{1}{x}$=$\frac{1}{y}$ | B. | 若x2=1,则x=1 | C. | 若$\sqrt{x}$=$\sqrt{y}$,则x=y | D. | 若x<y,则x2<y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com