
【题目】下列说法正确的是( )
A.“![]() ”是“点
”是“点![]() 到直线
到直线![]() 的距离为3”的充要条件
的距离为3”的充要条件
B.直线![]() 的倾斜角的取值范围为
的倾斜角的取值范围为![]()
C.直线![]() 与直线
与直线![]() 平行,且与圆
平行,且与圆![]() 相切
相切
D.离心率为![]() 的双曲线的渐近线方程为
的双曲线的渐近线方程为![]()
【答案】BC
【解析】
根据点到直线的距离公式判断选项A错误;根据直线斜率的定义及正切函数的值域问题判断选项B正确;根据两直线平行的判定及直线与圆相切的判定,可判断选项C正确;根据双曲线渐近线的定义可判断选项D错误.
选项A:由点![]() 到直线
到直线![]() 的距离为3,
的距离为3,
可得:![]() ,解得
,解得![]() 或
或![]() ,
,
“![]() ”是“点
”是“点![]() 到直线
到直线![]() 的距离为3”的充分不必要条件,
的距离为3”的充分不必要条件,
故选项A错误;
选项B:直线![]() 的斜率
的斜率![]() ,
,
设直线的倾斜角为![]() ,则
,则![]() 或
或![]() ,
,
![]() ,故选项B正确;
,故选项B正确;
选项C:直线![]() 可化为
可化为![]() ,
,
其与直线![]() 平行,
平行,
圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离为:
的距离为:
![]() ,
,
则直线![]() 与圆
与圆![]() 相切,故选项C正确;
相切,故选项C正确;
选项D:离心率为![]() ,则
,则![]()
若焦点在x轴,则双曲线的渐近线方程为![]() ,
,
若焦点在y轴,则双曲线的渐近线方程为![]() ,
,
故选项D错误.
故选:BC.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线
,准线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在抛物线上,直线
在抛物线上,直线![]() 与抛物线
与抛物线![]() 交于另一点
交于另一点![]() .
.

(1)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 常数;
常数;
(2)①设![]() 的内切圆圆心为
的内切圆圆心为![]() 的半径为
的半径为![]() ,试用
,试用![]() 表示点
表示点![]() 的横坐标
的横坐标![]() ;
;
②当![]() 的内切圆的面积为
的内切圆的面积为![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一所医院在某时间段为发烧超过38![]() 的病人特设发热门诊,该门诊记录了连续5天昼夜温差
的病人特设发热门诊,该门诊记录了连续5天昼夜温差![]() (
(![]() )与就诊人数
)与就诊人数![]() 的资料:
的资料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
昼夜温差 | 8 | 10 | 13 | 12 | 7 |
就诊人数 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并说明昼夜温差(
,并说明昼夜温差(![]() )与就诊人数
)与就诊人数![]() 具有很强的线性相关关系.
具有很强的线性相关关系.
(2)求就诊人数![]() (人)关于出昼夜温差
(人)关于出昼夜温差![]() (
(![]() )的线性回归方程,预测昼夜温差为9
)的线性回归方程,预测昼夜温差为9![]() 时的就诊人数.
时的就诊人数.
附:样本![]()
![]() 的相关系数为
的相关系数为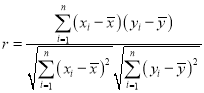 ,当
,当![]() 时认为两个变量有很强的线性相关关系.
时认为两个变量有很强的线性相关关系.
回归直线方程为![]() ,其中
,其中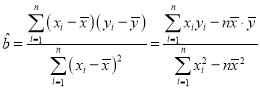 ,
,![]() .
.
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线的参数方程为
中,直线的参数方程为 (
(![]() 为参数).以原点为极点,轴正半轴为极轴建立极坐标系,曲线极坐标方程为
为参数).以原点为极点,轴正半轴为极轴建立极坐标系,曲线极坐标方程为![]() ,直线与曲线交于、两点.
,直线与曲线交于、两点.
(1)求直线的普通方程以及曲线的直角坐标方程;
(2)若直线上有定点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
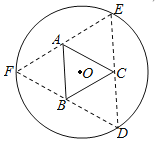
【题目】如图,圆形纸片的圆心为![]() ,半径为
,半径为![]() ,该纸片上的等边三角形
,该纸片上的等边三角形![]() 的中心为
的中心为![]() .
.![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的点,
上的点,![]() 分别是以
分别是以![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() 为折痕折起
为折痕折起![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合,得到三棱锥.当所得三棱锥体积(单位:
重合,得到三棱锥.当所得三棱锥体积(单位:![]() )最大时,
)最大时,![]() 的边长为_________(
的边长为_________(![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com