
(本小题满分12分)
已知函数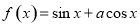
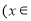 R
R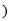 ,
,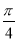 是函数
是函数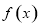 的一个零点.
的一个零点.
(1)求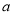 的值,并求函数
的值,并求函数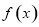 的单调递增区间;
的单调递增区间;
(2)若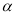
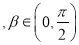 ,且
,且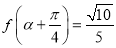 ,
,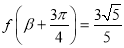 ,求
,求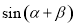 的值.
的值.
(1)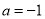 ,
,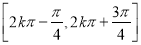
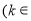 Z
Z ;(2)
;(2)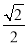 .
.
【解析】
试题分析:(1)由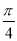 是函数
是函数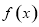 的一个零点得
的一个零点得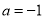 ,代入,用辅助角公式化简,得
,代入,用辅助角公式化简,得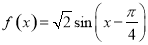
,利用正弦函数的单调递增区间即可求出函数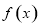 的单调递增区间;(2)先将已知条件进行化简,再利用
的单调递增区间;(2)先将已知条件进行化简,再利用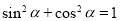 求出
求出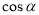 和
和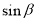 的值,进而
的值,进而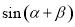 展开,代入数值.
展开,代入数值.
试题解析:(1)【解析】
∵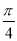 是函数
是函数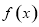 的一个零点,
的一个零点,
∴ 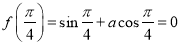 . 1分
. 1分
∴  . 2分
. 2分
∴ 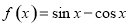
 3分
3分
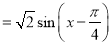 . 4分
. 4分
由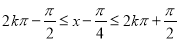 ,
,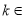 Z ,
Z ,
得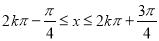 ,
,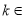 Z , 5分
Z , 5分
∴ 函数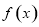 的单调递增区间是
的单调递增区间是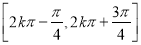
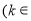 Z
Z . 6分
. 6分
(2)【解析】
∵ ,
,
∴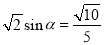 .
.
∴ 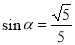 . 7分
. 7分
∵ 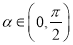 ,
,
∴ 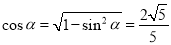 . 8分
. 8分
∵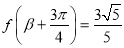 ,
,
∴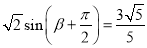 .
.
∴ 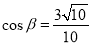 . 9分
. 9分
∵ 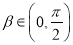 ,
,
∴ 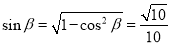 . 10分
. 10分
∴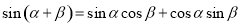 11分
11分
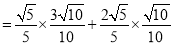
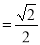 . 12分
. 12分
考点:1、函数的零点;2、辅助角公式;3、三角函数的单调性;4、诱导公式;5、同角三角函数的基本关系;6、两角和的正弦公式.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源:2014-2015学年山东省泰安市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
下列函数中,与函数 的奇偶性相同,且在
的奇偶性相同,且在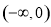 上单调性也相同的是
上单调性也相同的是
A.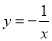 B.
B.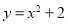
C.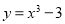 D.
D.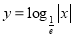
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知函数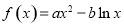 在点
在点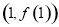 处的切线为
处的切线为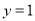 .
.
(1)求实数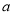 ,
, 的值;
的值;
(2)是否存在实数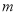 ,当
,当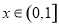 时,函数
时,函数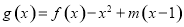 的最小值为
的最小值为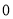 ,若存在,求出
,若存在,求出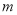 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)若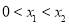 ,求证:
,求证: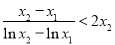 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟理科数学试卷(解析版) 题型:选择题
已知映射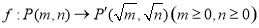 .设点
.设点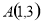 ,
,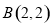 ,点
,点 是线段
是线段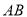 上一动点,
上一动点,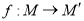 .当点
.当点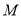 在线段
在线段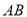 上从点
上从点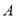 开始运动到点
开始运动到点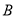 结束时,点
结束时,点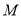 的对应点
的对应点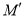 所经过的路线长度为( )
所经过的路线长度为( )
A.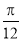 B.
B.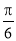 C.
C. 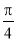 D.
D. 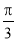
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com