
分析 (1)根据数列前4项猜想an=n+$\frac{1}{{2}^{n}}$;
(2)化简$\frac{10241}{1024}$=10+$\frac{1}{{2}^{10}}$,从而确定数列的项;
(3)记该数列的前10项和为S10,从而化简S10=1$\frac{1}{2}$+2$\frac{1}{4}$+3$\frac{1}{8}$+4$\frac{1}{16}$+…+10+$\frac{1}{{2}^{10}}$=1+2+3+…+10+($\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{10}}$),从而分别求和.
解答 解:(1)根据数列前4项1$\frac{1}{2}$,2$\frac{1}{4}$,3$\frac{1}{8}$,4$\frac{1}{16}$猜想an=n+$\frac{1}{{2}^{n}}$;
(2)$\frac{10241}{1024}$=10+$\frac{1}{{2}^{10}}$,
故$\frac{10241}{1024}$是该数列的第10项;
(3)记该数列的前10项和为S10,
S10=1$\frac{1}{2}$+2$\frac{1}{4}$+3$\frac{1}{8}$+4$\frac{1}{16}$+…+10+$\frac{1}{{2}^{10}}$
=1+2+3+…+10+($\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{10}}$)
=$\frac{1+10}{2}$×10+$\frac{\frac{1}{2}(1-\frac{1}{{2}^{10}})}{1-\frac{1}{2}}$
=55+1-$\frac{1}{{2}^{10}}$
=56-$\frac{1}{{2}^{10}}$=55$\frac{1023}{1024}$.
点评 本题考查了数列的通项公式的求法及前n项和公式的应用,同时考查了分类法的应用.


科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1,2} | B. | {-1,0,1} | C. | {-2,-1,1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | x=1,y=0 | C. | {(1,0)} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
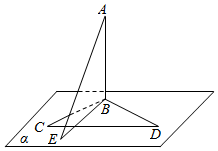 如图所示,在△BCD所在平面α内有一点E,BE=7cm,A为平面α外一点,AB⊥BC,AB⊥BD,且AB=5cm.
如图所示,在△BCD所在平面α内有一点E,BE=7cm,A为平面α外一点,AB⊥BC,AB⊥BD,且AB=5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com