
分析 (1)利用直线l:mx-y+1-m=0过定点P(1,1),而点P(1,1)在圆内,判定直线l与圆C总有两个不同交点A、B;
(2)设出弦AB中点M,用弦的中点与圆心连线与割线垂直,求出轨迹方程.
解答 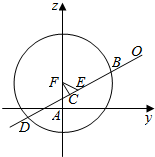 (1)证明:∵直线l:mx-y+1-m=0过定点P(1,1),而点P(1,1)在圆内,
(1)证明:∵直线l:mx-y+1-m=0过定点P(1,1),而点P(1,1)在圆内,
∴直线l与圆C总有两个不同交点;…(4分)
(2)解:当M与P不重合时,连结CM、CP,则CM⊥MP,
又因为|CM|2+|MP|2=|CP|2,
设M(x,y)(x≠1),则x2+(y-1)2+(x-1)2+(y-1)2=1,
化简得:x2+y2-x-2y+1=0(x≠1)…(7分)
当M与P重合时,x=1,y=1也满足上式.
故弦AB中点的轨迹方程是x2+y2-x-2y+1=0.…(9分)
点评 本题考查轨迹方程,直线和圆的方程的应用,考查转化思想,考查分析问题解决问题的能力,计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 26 | C. | 28 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
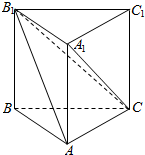 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有两个面平行,其余各面都是平行四边形的几何体叫棱柱 | |
| B. | 有一个面是多边形,其余各面都是三角形的几何体叫棱锥 | |
| C. | 由五个面围成的多面体一定是四棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{3}{2},2})$ | B. | $[{\frac{3}{2},2}]$ | C. | $({-\frac{1}{2},1}]$ | D. | $[{\frac{1}{2},2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com