
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
分析 设切点为(m,n),求出曲线对应函数的导数,可得切线的斜率,代入切点坐标,解方程可得n=0,进而得到2a+b=1,消去b,得到a的二次函数,即可得到所求最小值.
解答 解:设切点为(m,n),
y=ln(x+b)的导数为y′=$\frac{1}{x+b}$,
由题意可得$\frac{1}{m+b}$=1,
又n=m-2a,n=ln(m+b),
解得n=0,m=2a,
即有2a+b=1,即b=1-2a,
则$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{a}^{2}+(1-2a)^{2}}$
=$\sqrt{5{a}^{2}-4a+1}$=$\sqrt{5(a-\frac{2}{5})^{2}+\frac{1}{5}}$,
当a=$\frac{2}{5}$,b=$\frac{1}{5}$时,取得最小值$\frac{\sqrt{5}}{5}$.
故选:D.
点评 本题考查最值的求法,注意运用二次韩寒说的最值求法,同时考查导数的运用:求切线的斜率,注意设出切点,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
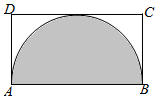 如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
如图所示,在矩形ABCD中,AB=2a,AD=a,图中阴影部分是以AB为直径的半圆,现在向矩形ABCD内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )| A. | 1000π | B. | 2000π | C. | 3000π | D. | 400π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 28 | C. | 30 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos(-α)=-cosα | B. | sin(-α)=-sinα | C. | sin(90°-α)=sinα | D. | cos(90°-α)=cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com