
分析 (1)由f(x)=x有唯一解,即为x-ax(x+2)=0有唯一解,运用判别式为0,求得a的值;
(2)求得x1=$\frac{2}{2005}$,xn+1=f(xn)=$\frac{2{x}_{n}}{2+{x}_{n}}$,取倒数,结合等差数列的定义和通项公式,即可得到所求;
(3)求出an=$\frac{4}{{x}_{n}}$-4009=2n+4008-4009=2n-1,由bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=1+$\frac{1}{3}$+…+($\frac{1}{3}$)n-1,运用等比数列的求和公式,求得cn=anbn=(2n-1)($\frac{3}{2}$-$\frac{1}{2•{3}^{n-1}}$)=3n-$\frac{3}{2}$-$\frac{1}{2}$(2n-1)•($\frac{1}{3}$)n-1,运用数列的求和方法:分组求和与错位相减法,结合等差数列和等比数列的求和公式,化简即可得到所求和.
解答 解:(1)f(x)=x即为f(x)-x=0,$\frac{x}{a(x+2)}$-x=0,
即有$\frac{x-ax(x+2)}{a(x+2)}$=0,即x-ax(x+2)=0,
f(x)=x有唯一解,即为x-ax(x+2)=0有唯一解,
即ax2+(2a-1)x=0有唯一解.
又∵a≠0.∴△=(2a-1)2=0,解得a=$\frac{1}{2}$;
(2)f(x1)=$\frac{2{x}_{1}}{2+{x}_{1}}$=$\frac{1}{1003}$,解得x1=$\frac{2}{2005}$,
xn+1=f(xn)=$\frac{2{x}_{n}}{2+{x}_{n}}$,取倒数可得$\frac{1}{{x}_{n+1}}$=$\frac{1}{{x}_{n}}$+$\frac{1}{2}$,
可得{$\frac{1}{{x}_{n}}$}成等差数列,且$\frac{1}{{x}_{1}}$=$\frac{2005}{2}$,
则$\frac{1}{{x}_{n}}$=$\frac{2005}{2}$+$\frac{1}{2}$(n-1)=$\frac{n+2004}{2}$,即有xn=$\frac{2}{n+2004}$;
(3)an=$\frac{4}{{x}_{n}}$-4009=2n+4008-4009=2n-1,
数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为$\frac{1}{3}$的等比数列,
可得bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=1+$\frac{1}{3}$+…+($\frac{1}{3}$)n-1=$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$=$\frac{3}{2}$-$\frac{1}{2•{3}^{n-1}}$,
cn=anbn=(2n-1)($\frac{3}{2}$-$\frac{1}{2•{3}^{n-1}}$)=3n-$\frac{3}{2}$-$\frac{1}{2}$(2n-1)•($\frac{1}{3}$)n-1,
前n项和Tn=3(1+2+…+n)-$\frac{3}{2}$n-$\frac{1}{2}$[1•($\frac{1}{3}$)0+3•($\frac{1}{3}$)+5•($\frac{1}{3}$)2+…+(2n-1)•($\frac{1}{3}$)n-1],
令Pn=1•($\frac{1}{3}$)0+3•($\frac{1}{3}$)+5•($\frac{1}{3}$)2+…+(2n-1)•($\frac{1}{3}$)n-1,①
$\frac{1}{3}$Pn=1•($\frac{1}{3}$)+3•($\frac{1}{3}$)2+5•($\frac{1}{3}$)3+…+(2n-1)•($\frac{1}{3}$)n,②
①-②可得$\frac{2}{3}$Pn=1+2[($\frac{1}{3}$)+($\frac{1}{3}$)2+…+($\frac{1}{3}$)n-1]-(2n-1)•($\frac{1}{3}$)n
=1+2[$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$]-(2n-1)•($\frac{1}{3}$)n,
化简可得Pn=$\frac{3}{2}$[2-(2n+2)•($\frac{1}{3}$)n],
∴Tn=3•$\frac{n(n+1)}{2}$-$\frac{3}{2}$n-$\frac{1}{2}$•$\frac{3}{2}$[2-(2n+2)•($\frac{1}{3}$)n]
=$\frac{3}{2}$n2+$\frac{3}{2}$n-$\frac{3}{2}$n-$\frac{3}{2}$+$\frac{n+1}{2•{3}^{n-1}}$
=$\frac{3}{2}$n2-$\frac{3}{2}$+$\frac{n+1}{2•{3}^{n-1}}$.
点评 本题考查函数与数理的综合应用,考查数列的通项公式和数列恒等式的运用,以及等比数列的求和公式,考查数列的求和方法:分组求和和错位相减法,综合性强,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
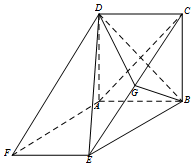 如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.
如图,ABCD是边长为3的正方形,ABEF是矩形,平面ABCD⊥平面ABEF,G为EC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com