
【题目】下列说法:
①若f(x)=ax2+(2a+b)x+2(其中x∈[﹣1,a])是偶函数,则实数b=﹣2;
②f(x)= ![]() +
+ ![]() 既是奇函数又是偶函数;
既是奇函数又是偶函数;
③若f(x+2)= ![]() ,当x∈(0,2)时,f(x)=2x , 则f(2015)=2;
,当x∈(0,2)时,f(x)=2x , 则f(2015)=2;
④已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R都满足f(xy)=xf(y)+yf(x),则f(x)是奇函数.其中所有正确命题的序号是 .
【答案】①②④
【解析】解:①由函数在区间[﹣1,a]上为偶函数可得:a=1,所以f(x)=x2+(2+b)x+2,
因为函数为偶函数,所以对称轴 ![]() ,故b=﹣2,故①正确;
,故b=﹣2,故①正确;
②易知函数的定义域为 ![]() ,此时f(x)=0,既是奇函数,也是偶函数,故②正确;
,此时f(x)=0,既是奇函数,也是偶函数,故②正确;
③由 ![]() ,可得
,可得 ![]() ,故函数为周期为4的周期函数,所以f(2015)=f(3),
,故函数为周期为4的周期函数,所以f(2015)=f(3),
又f(3)=f(1+2)= ![]() =
= ![]() ,即
,即 ![]() ,故③错误;
,故③错误;
④令x=y=1,可得:f(1)=0,令x=y=﹣1,得f(1)=﹣f(﹣1)﹣f(﹣1),故f(﹣1)=0,
令y=﹣1可得:f(﹣x)=xf(﹣1)﹣f(x)=﹣f(x),
故函数为奇函数,所以④正确.
所以答案是:①②④.
【考点精析】本题主要考查了命题的真假判断与应用和函数的奇偶性的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
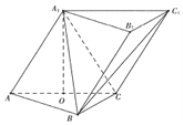
(Ⅰ)证明:A1O⊥平面ABC;
(Ⅱ)求三棱锥C1﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若函数f(x)满足条件:存在[a,b]D,使f(x)在[a,b]上的值域是[2a,2b],则称f(x)为“倍扩函数”,若函数f(x)=log2(2x+t)为“倍扩函数”,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中:
①为了了解800名学生对学校某项教改试验的意见,打算从中抽取一个容量为40的样本,考虑用系统抽样,则分段的间隔k为40.
②线性回归直线方程 ![]() 恒过样本中心(
恒过样本中心( ![]() ,
, ![]() ),且至少过一个样本点;
),且至少过一个样本点;
③在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4;
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接中国共产党的十九大的到来,某校举办了“祖国,你好”的诗歌朗诵比赛.该校高三年级准备从包括甲、乙、丙在内的7名学生中选派4名学生参加,要求甲、乙、丙这3名同学中至少有1人参加,且当这3名同学都参加时,甲和乙的朗诵顺序不能相邻,那么选派的4名学生不同的朗诵顺序的种数为( )
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+b(a>0)在区间[﹣1,4]上有最大值10和最小值1.设g(x)= ![]() .
.
(1)求a、b的值;
(2)证明:函数g(x)在[ ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(3)若不等式g(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=log4(4x+1)+ax(a∈R).
(1)若函数f(x)是定义在R上的偶函数,求a的值;
(2)若不等式f(x)+f(﹣x)≥mt+m对任意x∈R,t∈[﹣2,1]恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com