
分析 利用等比数列前n项和公式求出首项及公比,由此能求出等比数列的前n项和的极限.
解答 解:∵无穷等比数列{an}的前n项和为Sn,若S3=6,S6=3,
∴$\left\{\begin{array}{l}{{S}_{3}=\frac{{a}_{1}(1-{q}^{3})}{1-q}=6}\\{{S}_{6}=\frac{{a}_{1}(1-{q}^{6})}{1-q}=3}\end{array}\right.$,解得${a}_{1}=4+2\root{3}{4}$,q=-$\frac{\root{3}{4}}{2}$,
∴Sn=$\frac{(4+2\root{3}{4})[1-(-\frac{\root{3}{4}}{2})^{n}]}{1+\frac{\root{3}{4}}{2}}$,
∴$\underset{lim}{n→∞}{S}_{n}$=$\underset{lim}{n→∞}$$\frac{(4+2\root{3}{4})[1-(-\frac{\root{3}{4}}{2})^{n}]}{1+\frac{\root{3}{4}}{2}}$=$\frac{4+2\root{3}{4}}{1+\frac{\root{3}{4}}{2}}$=$\frac{8+4\root{3}{4}}{2+\root{3}{4}}$.
故答案为:$\frac{8+4\root{3}{4}}{2+\root{3}{4}}$.
点评 本题考查等比数列的前n项和的极值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数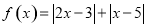 .
.
(1)求不等式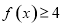 的解集;
的解集;
(2)若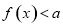 的解集不是空集,求实数
的解集不是空集,求实数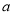 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若直线与平面没有公共点,则它们平行 | |
| B. | 如果两直线没有公共点,那么这两直线平行 | |
| C. | 若两平面没有公共点,则它们平行 | |
| D. | 若一个平面经过另一个平面的一条垂线,则这两个平面垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com