
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
分析 由已知数列递推式结合首项求出数列前几项,可得数列{an}是以3为周期的周期数列,由此求得a2012的值.
解答 解:由已知数列递推式an+1=$\left\{\begin{array}{l}2{a_n}({0≤{a_n}<\frac{1}{2}})\\ 2{a_n}-1({\frac{1}{2}≤{a_n}<1})\end{array}$,且a1=$\frac{6}{7}$,
求得${a}_{2}=\frac{5}{7}$,${a}_{3}=\frac{3}{7}$,${a}_{4}=\frac{6}{7}$,…
由上可知,数列{an}是以3为周期的周期数列,
则a2012=${a}_{3×670+2}={a}_{2}=\frac{5}{7}$.
故选:C.
点评 本题考查数列递推式,关键在于对数列周期的发现,是基础题.


科目:高中数学 来源:2017届河南新乡一中高三9月月考数学(文)试卷(解析版) 题型:选择题
在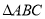 中,角
中,角 ,
,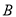 ,
,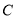 的对边分别是
的对边分别是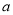 ,
,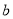 ,
,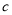 ,
, 为
为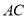 边上的高,
边上的高,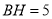 ,若
,若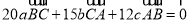 ,则
,则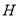 到
到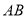 边的距离为( )
边的距离为( )
A.2 B.3 C.1 D.4
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -9 | C. | 3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com