
已知函数f(x)=x3+ax2+bx+c在x=-1与x=2处都取得极值.
(1)求a,b的值及函数f(x)的单调区间;
(2)若对x∈[-2,3],不等式f(x)+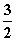 c<c2恒成立,求c的取值范围.
c<c2恒成立,求c的取值范围.
解 (1)f′(x)=3x2+2ax+b,由题意得
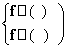 即
即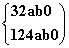 解得
解得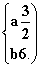
∴f(x)=x3-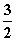 x2-6x+c,f′(x)=3x2-3x-6.
x2-6x+c,f′(x)=3x2-3x-6.
令f′(x)<0,解得-1<x<2;
令f′(x)>0,解得x<-1或x>2.
∴f(x)的减区间为(-1,2),
增区间为(-∞,-1),(2,+∞).
(2)由(1)知,f(x)在(-∞,-1)上单调递增;
在(-1,2)上单调递减;在(2,+∞)上单调递增.
∴x∈[-2,3]时,f(x)的最大值即为
f(-1)与f(3)中的较大者.
f(-1)=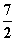 +c,f(3)=-
+c,f(3)=-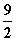 +c.
+c.
∴当x=-1时,f(x)取得最大值.
要使f(x)+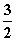 c<c2,只需c2>f(-1)+
c<c2,只需c2>f(-1)+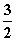 c,
c,
即2c2>7+5c,解得c<-1或c>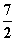 .
.
∴c的取值范围为 (-∞,-1)∪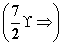 .
.


科目:高中数学 来源: 题型:
如图所示,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高度是60 m,则河流的宽度BC等于( )
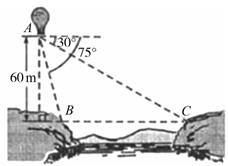

A.240(-1)m B.180(-1)m
C.120(-1)m D.30(+1)m
查看答案和解析>>
科目:高中数学 来源: 题型:
在空间中,a,b表示直线,a,b 表示平面,下列命题中正确的是( )
A.若a∥a,b∥a,则b∥a B.若a∥a,b∥a,aÌb,bÌb,则b∥a
C.若a∥b,b∥a,则b∥b D.若a∥b,aÌa,则a∥b
查看答案和解析>>
科目:高中数学 来源: 题型:
在实验室进行的一项物理实验中,要先后实施6个程序,其中程序A只能出现在第一或最后一步,程序B和C在实施时必须相邻,则实验顺序的编排方法共有( )
A.34种 B.48种 C.96种 D.144种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com