
【题目】如图,正方体![]() 的棱长为1,
的棱长为1,![]() 为
为![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]()
![]()
![]() 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为![]() ,给出下列三个结论:
,给出下列三个结论:
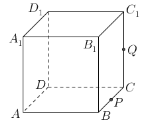
① 当![]() 时,
时,![]() 为四边形;
为四边形;
② 当![]() 时,
时,![]() 为等腰梯形;
为等腰梯形;
③ 当![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
以上结论正确的个数是( )
A.0B.1C.2D.3
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学文化的优秀遗产,数学家刘徽在注解《九章算术》时,发现当圆内接正多边行的边数无限增加时,多边形的面积可无限逼近圆的面积,为此他创立了割圆术,利用割圆术,刘徽得到了圆周率精确到小数点后四位3.1416,后人称3.14为徽率,如图是利用刘徽的割圆术设计的程序框图,若结束程序时,则输出的![]() 为( )(
为( )(![]() ,
,![]() ,
,![]() )
)
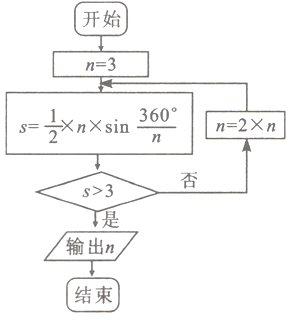
A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)至少有6个零点,则a的取值范围是( )
A.(0,![]() )B.(0,
)B.(0,![]() )C.(0,
)C.(0,![]() )D.(0,
)D.(0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】方程为![]() 的曲线,给出下列四个结论:
的曲线,给出下列四个结论:
① 关于![]() 轴对称;
轴对称;
② 关于坐标原点对称;
③ 关于![]() 轴对称;
轴对称;
④ ![]() ,
,![]() ;
;
以上结论正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=AC,∠ACB的平分线与AB交于点D,过△ABC的外心O作CD的垂线与AC交于点E,过E作AB的平行线与CD交于点F。证明:

(1)C、E、0、F四点共圆;
(2)A、0、F三点共线;
(3)EA=EF。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数
对其公共定义域上的任意实数![]() 都满足:
都满足:![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
,![]() ,
,![]() ,下列命题为真命题的是( )
,下列命题为真命题的是( )
A.![]() 在
在![]() 内单调递减
内单调递减
B.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为
的最小值为![]()
C.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]()
D.![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】罗马数字是欧洲在阿拉伯数字传入之前使用的一种数码,它的产生标志着一种古代文明的进步.罗马数字的表示法如下:
数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
形式 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ |
其中“Ⅰ”需要1根火柴,“Ⅴ”与“X”需要2根火柴,若为0,则用空位表示. (如123表示为![]() ,405表示为
,405表示为![]() )如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
)如果把6根火柴以适当的方式全部放入下面的表格中,那么可以表示的不同的三位数的个数为( )
![]()
A.87B.95C.100D.103
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的焦点,若点
的焦点,若点![]() 在抛物线
在抛物线![]() 上,且
上,且![]()
![]() 求抛物线
求抛物线![]() 的方程;
的方程;
![]() 动直线
动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() 其中
其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线
共线![]() 其中
其中![]() 为坐标原点
为坐标原点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com