
���� �ɷֶκ��������bn=a${\;}_{{2}^{n-2}+1}$�����ɺ���fn��x�������n=1ʱ��a1=1����n��Ϊn-1������ɵ�an=2n-1�������õ�
bn=2n-1+1���������е���ͷ�����������ͣ���ϵȱ����е����ʽ�����㼴�ɵõ�����ͣ�
��� �⣺�ɺ���g��n��=$\left\{\begin{array}{l}{{a}_{n}��nΪ����}\\{g��\frac{n}{2}����nΪż��}\end{array}\right.$��
�ɵ�bn=g��2n+4��=g��2n-1+2��=g��2n-2+1��=a${\;}_{{2}^{n-2}+1}$��
�ɺ���fn��x��=a1x+a2x2+a3x3+��+anxn����fn��-1��=��-1��nn��
�ɵ�-a1+a2-a3+��+an��-1��n=��-1��nn����
n=1ʱ��-a1=-1���ɵ�a1=1��
n��2ʱ��-a1+a2-a3+��+an-1��-1��n-1=��-1��n-1��n-1������
��-�ڿɵ�an��-1��n=��-1��nn-��-1��n-1��n-1����
����ɵ�an=2n-1����n=1Ҳ������
bn=g��2n+4�����ɵ�b1=g��6��=g��3��=a3=5��
b2=g��8��=g��4��=g��2��=g��1��=a1=1��
b3=g��12��=g��6��=g��3��=a3=5��
��bn=a${\;}_{{2}^{n-2}+1}$=2n-1+1��n��3��
������{bn}��ǰn��n��2�����Sn����5+1+��4+��+2n-1��+n-2
=6+4•$\frac{1-{2}^{n-2}}{1-2}$+n-2=2n+n��
�ʴ�Ϊ��$\left\{\begin{array}{l}{6��n=2}\\{{2}^{n}+n��n��3}\end{array}\right.$��
���� ���⿼�����е���ͣ�������ͣ�ע�����õȱ����е����ʽ������ֶκ�����Ӧ�ã�����ת��˼��ͻ������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
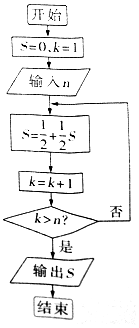 ׯ��˵����һ��֮������ȡ��룬�������ߡ�����仰��������һ���������⣬���ó����ͼ��������ͼ��ʾ��������ij��������n�������S�ʣ�$\frac{15}{16}$��$\frac{63}{64}$�����������n��ֵΪ��������
ׯ��˵����һ��֮������ȡ��룬�������ߡ�����仰��������һ���������⣬���ó����ͼ��������ͼ��ʾ��������ij��������n�������S�ʣ�$\frac{15}{16}$��$\frac{63}{64}$�����������n��ֵΪ��������| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��3�� | B�� | {1��3} | C�� | ��5��7�� | D�� | {5��7} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -$\frac{5\sqrt{2}+1}{7}$ | C�� | $\frac{1}{3}$ | D�� | -$\frac{7}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 31 | B�� | 32 | C�� | 61 | D�� | 62 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
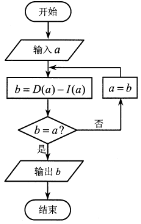 ��a��һ����λ���ֶ�����0��û���ظ����ֵ���λ���������a��3�����ְ���С�����ųɵ���λ����ΪI��a�������Ӵ�С�ųɵ���λ����ΪD��a����������a=746��
��a��һ����λ���ֶ�����0��û���ظ����ֵ���λ���������a��3�����ְ���С�����ųɵ���λ����ΪI��a�������Ӵ�С�ųɵ���λ����ΪD��a����������a=746���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36 | B�� | 72 | C�� | C144 | D�� | 288 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com