
分析 根据对数的性质可知ax2-2x+4>0,函数y=ax2-2x+4的最小值为1.可得a的值.
解答 解:由题意,函数f(x)=log${\;}_{\frac{1}{2}}$(ax2-2x+4)
∵f(x)的值域为(-∞,1],
∴ax2-2x+4>0,函数y=ax2-2x+4的最小值为$\frac{1}{2}$,
即$\left\{\begin{array}{l}{a>0}\\{4×4a-(-2)^{2}=2a}\end{array}\right.$,
可得:a=$\frac{2}{7}$.
故答案为:$\frac{2}{7}$.
点评 本题考查了对数函数的运用和性质以及复合函数的值域问题.属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正确 | B. | 因大前提错误导致结论出错 | ||
| C. | 因小前提导致结论出错 | D. | 因推理形式错误导致结论出错 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
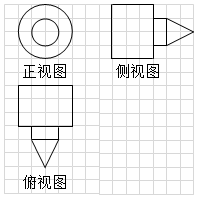 放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(
放烟花是逢年过节一种传统庆祝节日的方式.已知一种烟花模型的三视图如图中的粗实线所示,网格纸上小正方形的边长为1,则该烟花模型的表面积为(| A. | $(18+\sqrt{3})π$ | B. | $(21+\sqrt{3})π$ | C. | $(18+\sqrt{5})π$ | D. | $(21+\sqrt{5})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1]$ | B. | $(\frac{{12\sqrt{5}}}{5}-1,\frac{{12\sqrt{5}}}{5}+1)$ | C. | $[12-\sqrt{5},12+\sqrt{5}]$ | D. | $(12-\sqrt{5},12+\sqrt{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com